雨の日は歩くのと走るのどっちが濡れない？【数式・モデル】

雨に悩まされることが多い梅雨 rainy/monsoon/wet season^[1]梅雨を示す決まった英語はない。また日本語で別名、五月雨ともや台風 typhoon^[2]語源が日本語と英語で同じという説がある。の季節。
そんな雨の日には誰しも「歩いた方が濡れるのか、それとも走った方が濡れるのか？」という疑問を抱いたことがあるのではないでしょうか？

今回は、そんな素朴な疑問を高校までの知識と簡単なモデルを使って解決しました。数学や物理に関心のある人も納得してもらえるように、数式多めで解説したいと思います。

雨の中を移動するモデルを作る

式を作って解く前に、人が雨に濡れるという複雑な現象を簡単なモデルに置き換えて考えていきます。

まずは人間のモデル化から行います。なるべく簡単であるほど計算しやすいので、縦l、横w、高さhの直方体だとします。それぞれの文字の意味はlength(縦)、width(横)、height(高さ)の頭文字を採用しています。

直方体に簡略化した人間は細長い豆腐みたいなので、これ以降は豆腐人間とでも言うことにしましょう。

豆腐人間は速度|\boldsymbol{v}|でx軸上を0からL[m]まで移動するとします。
私たちが現実に歩く際はy軸やz軸方向にも移動しますが、急に曲がったり坂道を登り降りする時以外は、ほぼ平面的かつ直線運動をしているはずです。なので今回のモデルでは、豆腐人間の移動をx方向の1次元だけに限定することにします。

次に、風が吹く中で雨が降ることをモデルに落とし込みます。風がないときに雨はx軸に垂直に落下しますが、台風などで風が強い日は横殴りに降るので、雨の速度\boldsymbol{v}_{rain}をx,z成分を持つベクトルで考えます。こちらも人が歩くときと同じようにy成分を考えてもいいのですが、計算を簡単にするために無視します。
また、雨粒の密度は1\text{m}^{3}あたりn個含まれているとします。

ここまでを図に表すとこうなります。

実際の計算に移る前に、豆腐人間に当たる雨の運動を慣性系で考えます。速度\boldsymbol{v}で歩行する豆腐人間から見ると、雨は\boldsymbol{v}_{rain}と\boldsymbol{v}の二つのベクトルを合成した

\boldsymbol{v}_0=\boldsymbol{v}_{rain}+\boldsymbol{v} \ [\text{m}/\text{s}]

の速度で当たっているように見えます。図示すると下の通りです。

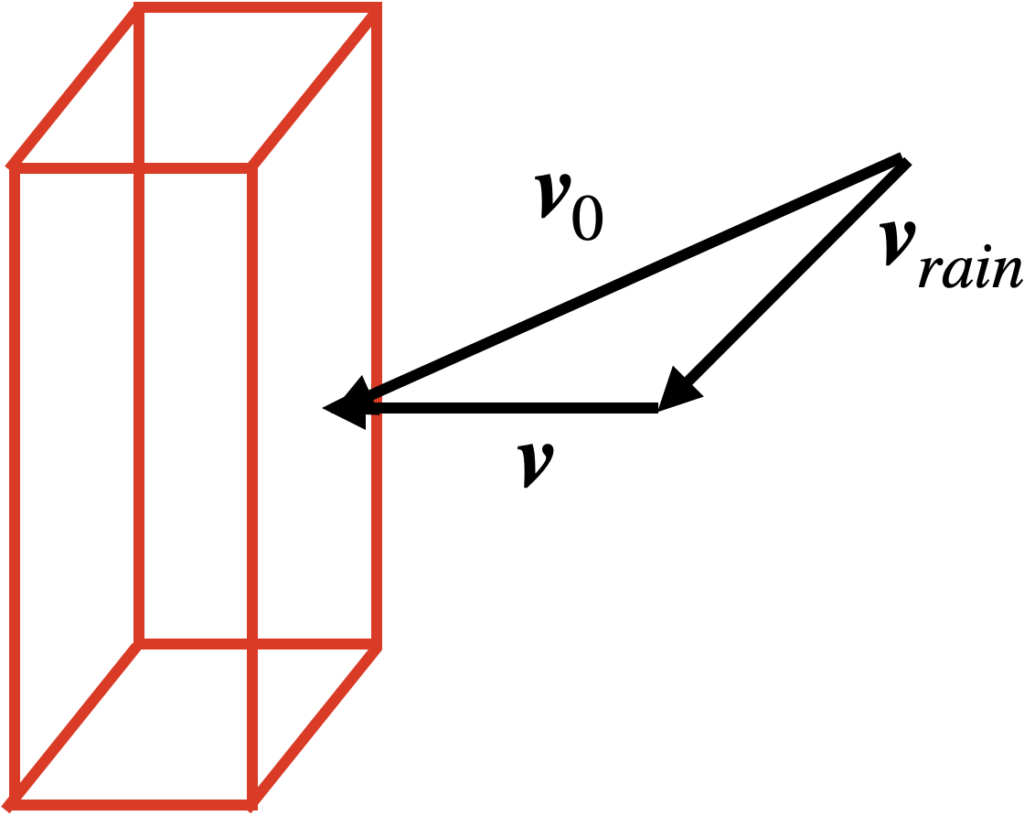
これで雨に濡れた人のモデルが出来ました。次の章で、今作ったモデルを元にして式をたてていきましょう。

豆腐人間にあたる雨粒の個数を求める

それでは、単位時間あたりに豆腐人間にあたる雨粒の個数を求めます。
まず、速度ベクトル\boldsymbol{v}_0をx軸方向とy軸方向に分解します。

分解した速度ベクトルの水平成分と垂直成分の式は下の通りです。

\begin{aligned}
& v_\text{h}=|\boldsymbol{v}|+|\boldsymbol{v}_{rain}|\text{sin}\theta \ [\text{m}/\text{s}]\\
& v_\text{v}=|\boldsymbol{v}_{rain}|\text{cos}\theta \ [\text{m}/\text{s}]
\end{aligned}

説明不要かもしれませんが、v_\text{h}, v_\text{v}の右下についた文字(添え字)の意味は水平 horizontal、垂直 verticalの頭文字で、|\boldsymbol{v}|は速度の絶対値という意味です。

今回考えたモデルでは|\boldsymbol{v}|はx方向の成分しかないのでv_\text{h}にだけ使いますが、もし豆腐人間が坂道を登ったりするようなz成分への運動をしている場合、v_\text{v}の中身にも|\boldsymbol{v}|の成分が入ってきます。

分解した水平方向と垂直方向の速度成分を使って、豆腐人間の頭と側面に1秒間に当たる雨粒の個数N_sを求めます。雨粒の密度と分解した雨の速度、それから豆腐人間の頭頂と雨の当たる側面の面積を掛け合わせて下のような式になります。上から順番に見ていってください。

\begin{aligned}
& \left( wlv_\text{v}+hlv_\text{h} \right) \times n=N_s[\text{count}/\text{s}] \\[3mm]
& \left( wl|\boldsymbol{v}_{rain}|\text{cos}\theta+ hl(|\boldsymbol{v}|+|\boldsymbol{v}_{rain}|\text{sin}\theta) \right)n=N_s[\text{count}/\text{s}] \\[3mm]
& \left( |\boldsymbol{v}_{rain}|(wl\text{cos}\theta+hl\text{sin}\theta)+ |\boldsymbol{v}|hl \right) n=N_s [\text{count}/\text{s}]\\[3mm]
\end{aligned}

式をさっくり説明すると、左辺の[]内の式で「豆腐人間からみて」豆腐人間が受ける雨の正味の空間の体積を計算しています。そして、その空間の中では密度n [\text{m}^3/ \text{s}]の雨が含まれているので、それらを掛け合わせることで一秒間に当たる雨粒の個数を求めています。

この式が本当に1秒間に当たる雨粒なのか気になる人は、上のどの式でもいいので、左辺と右辺の単位を計算して同じになっているか確認してみましょう。

今回は、一番上の簡単な式を使って単位の確認を行います。

\begin{aligned}
& \left(wlv_\text{v}+hlv_\text{h}\right )\times n
=N_s[\text{count}/\text{s}] \\[3mm]
& \downarrow \\[3mm]
& 左辺の単位\\[3mm]
& = [\text{m} \times \text{m} \times \text{m/s} + \text{m} \times \text{m} \times \text{m/s}] \times [\text{count}/ \text{m}^3] \\[3mm]
& = 2 \times [\text{m}^3/\text{s}] \times [\text{count}/\text{m}^3] \\[3mm]
& = 2 \times[\text{count/s}] \\[3mm]
& = 2[\text{count}/\text{s}] \\[3mm]
& =右辺の単位
\end{aligned}

最後に2という係数がつきましたが、確認するべきなのは単位なので数字は無視して大丈夫です。ちゃんと左辺と右辺の単位が合致していましたね。このように、単位を確認することは、求めたい量を表す式になっているのかを確認する一つの手段です。

次に、地点Lまで移動したときに当たった雨粒の総数N_{all}を求めるには、上の式に移動時間Tをかけます。

T=\frac{L}{|\boldsymbol{v}|} \ [\text{s}]\\[3mm]
\left ( |\boldsymbol{v}_{rain}|(wl\text{cos}\theta+hl\text{sin}\theta)n+hl|\boldsymbol{v}|n \right) T \equiv N_{all}\ [\text{count}]\\[5mm]
\left( \frac{ |\boldsymbol{v}_{rain}| }{ |\boldsymbol{v}| }( wl \text{cos} \theta +hl \text{sin} \theta )+hl \right) nL \equiv N_{all} \ [\text{count}]

以上で欲しい式が求められました。気になる人は単位を確認してみると良いかもしれません。

文字で書くとなんだか仰々しく見えますが、よく見ると大したことはない？と思います。気になる人は単位と一緒に式の内容を確認してみてください。

グラフ化して特性を見る

数式だけではイメージが湧きにくい部分もあるかと思うので、求めた式に数値を代入して、豆腐人間に当たる雨粒の個数がどのように変化するかをグラフにします。
暫定的な初期値を決めるために、まずは下のリストのような値にします。

• l=0.30 [\text{m}]
• w=0.50 [\text{m}]
• h=1.70 [\text{m}]
• v=1.40 [\text{m} / \text{s}]
• L=100 [\text{m}]
• n=20\text{M}=20,000,000[個/\text{m} ^3]
• |\boldsymbol{v}_{rain}| =8 [\text{m} / \text{s}]
• \theta=45[^\circ]

その上で雨があたる角度によって雨粒の総数N_{all}がどのように変化するかを見てみましょう。

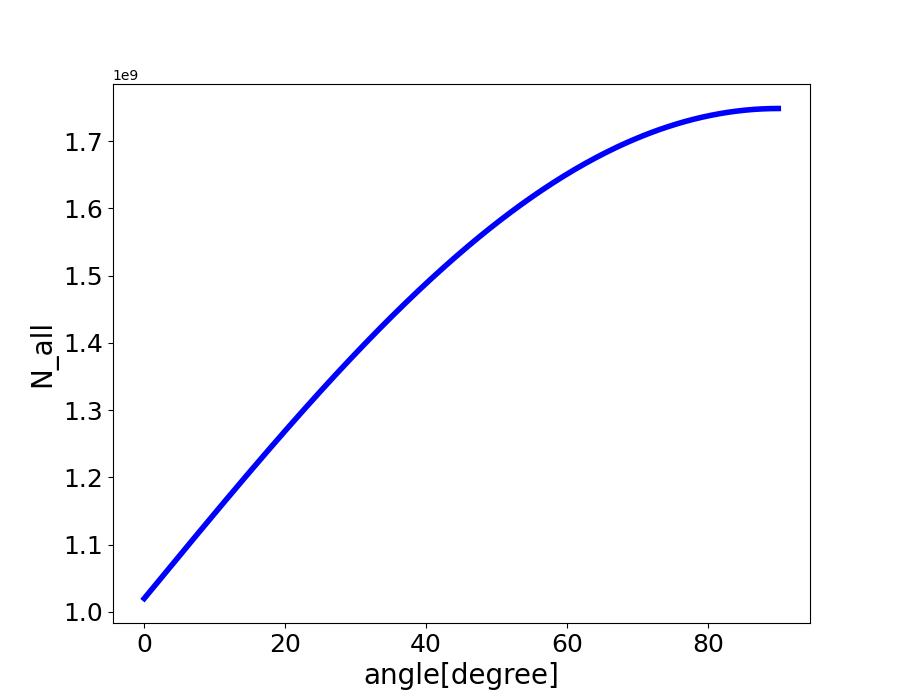
ご覧の通り、\thetaが大きくなると雨粒のあたる数はsin関数の形で増加しています。

\thetaが大きくなるということは、雨の速度のうちx軸に水平な成分、つまり横向きの成分が大きくなるということです。
物理的には、風の影響で雨が横殴りに降っていることを意味しており、豆腐人間の側面に多くの雨粒が当たります。人間は側面の表面積が大きいので自然と多くの雨粒にあたり、N_{all}が大きくなるのです。

小難しく書きましたが、横殴りの雨は良く濡れるということが数式から導けたということになります。

続いて角度を\theta=45[^\circ]に固定して、豆腐人間の歩く速度を0~10[\text{m/s}]まで変化させたときの雨粒のあたる数をグラフにしてみます。10[\text{km/s}]はもはや短距離選手の走る速度なので歩くではないですが、今回はなるべく簡単な数値で考えるためにこのようにしました。
まず、1秒間にあたる雨粒の数N_{s}のグラフを描画しました。

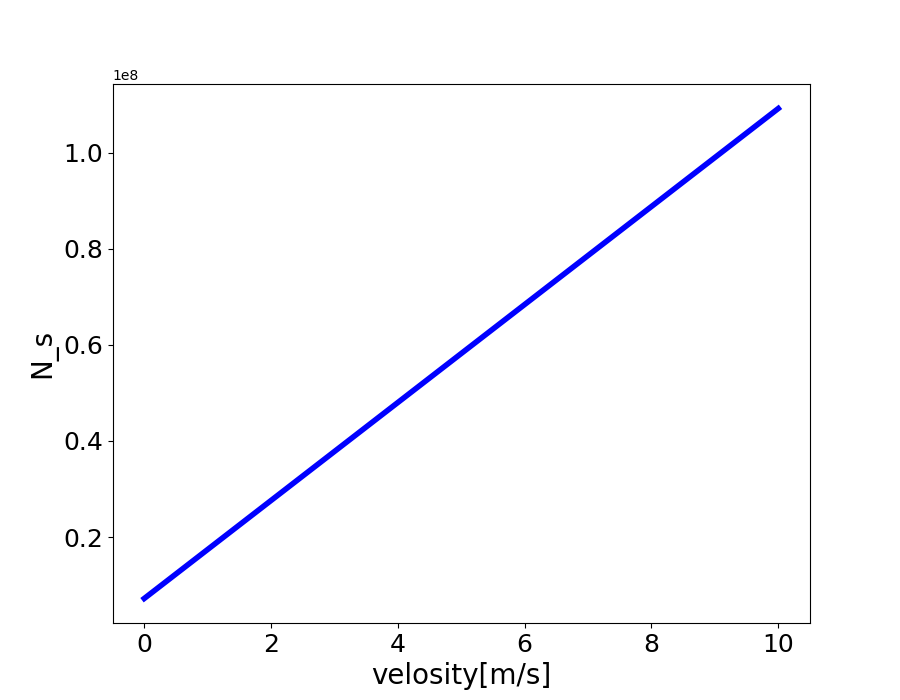
綺麗な比例のグラフになっています。数式に見慣れている人はグラフを見なくてもわかったかもしれません。歩行速度が上がるということは、豆腐人間が自分から雨にぶつかりにいく速度が上がるということであり、1秒間あたりの雨粒の当たる数は大きくなります。

続いて、豆腐人間が地点Lまでに当たった雨粒の総数N_{all}をグラフにするとこうなります。

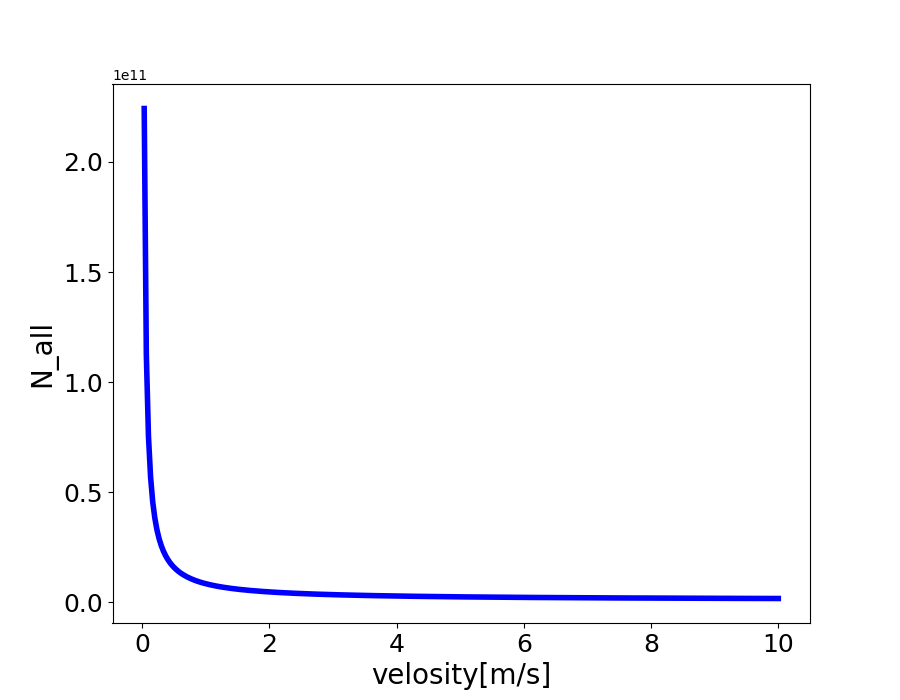
グラフから明らかなように、速度が上がるとN_{all}は急速に減衰しています。速度0[\text{m/s}]とは雨の中突っ立ったままという意味なので、いつまで経っても地点Lまで到着せず無限大に発散します。逆に速度が大きくなるほど雨の総量は0に収束します。

実際の人間が雨の中を移動する速度は大体0.5~2[\text{m/s}]でしょうから、上のグラフからその部分を抜き出してみます。

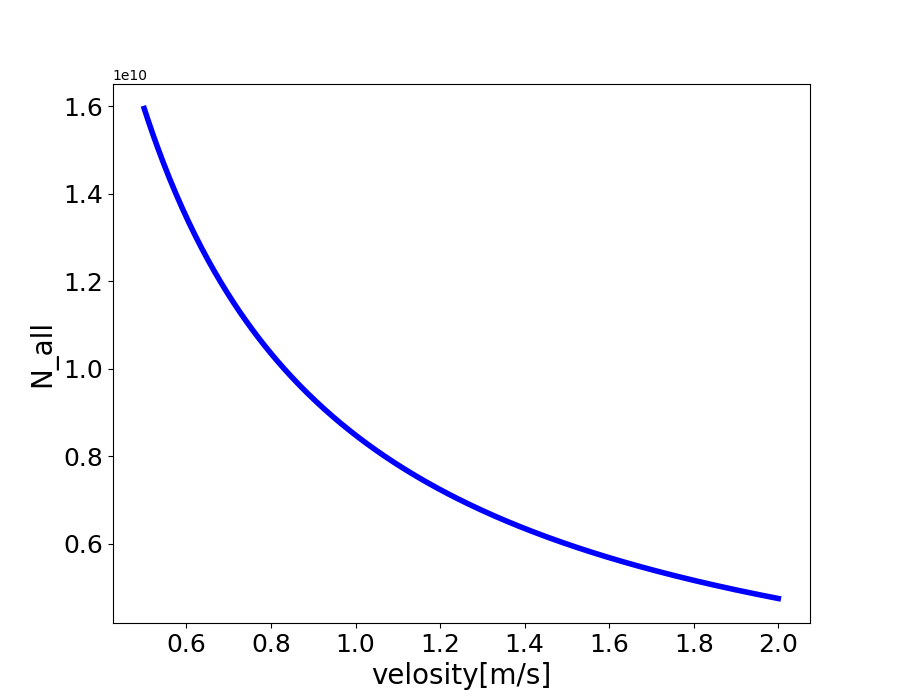
値を確認してみます。まず0.9[\text{m/s}](=3.24[\text{km/h}])で歩いたときは約0.93\times 10^{10}個で、1.8[\text{m/s}](=6.48[\text{km/h})で走ったときは約0.51\times 10^{10}個でした。

歩行速度が2倍になると、あたる雨粒の総量はおよそ1/2倍になっており、移動速度と雨粒の送料にはおよそ反比例の関係があることがわかります。

つまり、早く移動する方が雨にあまり当たらずにすむということです。
歩く速度が上がれば、豆腐人間の側面に1秒間にあたる雨粒は増えますが、その分早く到着するので最終的に早く移動したほうが良いという結論になります。

まとめ

今回の記事で使った式は次の2つでした。

\left ( |\boldsymbol{v}_{rain}|(wl\text{cos}\theta+hl\text{sin}\theta)+ |\boldsymbol{v}|hl \right ) n=N_s \ [\text{count/s}]\\[3mm]
\left ( \frac{ |\boldsymbol{v}_{rain}| }{ |\boldsymbol{v}| }( wl \text{cos} \theta +hl \text{sin} \theta )+hl \right ) nL \equiv N_{all} \ [\text{count}]

式からわかる重要な2つの点は

• 横殴りの雨ほど濡れる。
• 早く移動するほど、最終的に濡れる量は少ない。

です。単純なモデルでしたが、早く移動した方が濡れないという大体の傾向は掴むことができました。

この記事が面白いと思った方は、式を読み返したりモデルを改良してみましょう。モデルの改良点として例えばこんなものがあります。

• 豆腐人間の移動や雨の運動を3次元的にしてみる。
• 豆腐人間をもっと複雑にしたり、あるいは全く別の形にする。
• 水溜りや歩行による水はねを考慮する。
• 傘を持った時と持たない時の比較

モデルを改良したら数式やグラフからどんなことがわかるか考えてみてください。きっと自分だけの新しい発見があるはずです。

当サイトで取り上げた記事のほか、Twitter でもさまざまな情報を発信していますのでよろしければフォローをお願いします。

マサ: @masa_fpp03