量子力学に出てくる、重要かつ基礎的な用語・方程式・概念をまとめました。
- 量子力学に何となく興味がある人
- 量子力学の勉強の入り口に立ちたい人
- 何から勉強すればいいか分からない人
- 量子力学を学び始めていて、用語の確認をしたい人
へ向けて、量子力学の外観を少しでも知ってもらえたらと思います。
式番号は上から順についていますが、気にせず知りたい項目からご覧ください。
他の記事の公開などに伴って、随時追記していく予定です。
量子 Quantum
量子力学では、これまで無視してきた原子一粒ほどの小さな物質の運動に焦点を当てます。
そこでのあらゆる現象は私たちが普段生活している世界とは根本的に違い、量子の世界の粒子や波動はお互いに波と粒子の性質を合わせ持ちます(波動と粒子の二重性)。
この波と粒の性質を合わせ持った小さな物質やエネルギーを量子と呼びます。
量子に関する詳しい説明はこちらの記事にまとめています。
 量子 Quantum ってなんだろう?
量子 Quantum ってなんだろう? 波動性と粒子性 Wave/particle nature
光や電子は「波動」と「粒子」の二つの性質を合わせ持ちます。この性質を発見した実験の一つが二重スリット実験です。
現象に応じて、波動性と粒子性のうちどちらか一方の性質だけが顕在化することがあります。
人間は光や電子の実態を観測できませんが、それらが作り出す量子現象には、ほぼ確実に二つの性質が根底にあります。
量子の持つ波動性と粒子性については、二重スリット実験を例に説明したこちらの記事が参考になります。
 波動性と粒子性とは/二重スリット実験から多世界解釈まで
波動性と粒子性とは/二重スリット実験から多世界解釈まで 波動関数 Wave function
ニュートン力学には登場しない量子力学特有の概念で、「状態」を記述した関数です。
F=maなどの古典物理学の運動方程式では、状態自体を表した物理量(長さ、質量、時間など)や関数はありません。
しかし、量子力学の中では抽象的な状態そのものを関数として導入しています。
以下の式のように、位置と時間の関数 \phi, \psi で書かれることが多いです。
\phi(\boldsymbol{r},t), \psi(\boldsymbol{r},t)確率解釈 Stochastic interpretation
波動関数は一般的に複素数であり、私たちの見ている世界では観測することができません。
しかし、波動関数に複素共役を取ったものと、元の波動関数を掛けると虚数が消え、正の実数となるので観測可能になります。この操作は波動関数に絶対値を取って二乗することと同じです。
すると波動関数の二乗絶対値した値と一体何なのか、私たちが観測可能な量とどんな関係があるのか、量子力学の成立に伴っていくつかの解釈が提唱されました。
その中で現在最もされているのが(ボルンの)確率解釈です。この説によると波動関数の二乗絶対値がその位置に粒子が存在する確率を表します。
粒子がある位置\boldsymbol xに存在する確率密度 probability densityを\rho、波動関数を\phi(x)として確率解釈を式に表すと下のように書けます。
\begin{equation}
\rho(x)=\phi^*(x)\phi(x) \\[4mm]
=|\phi(x)|^{2}
\end{equation}\phi^*(x)は\phi(x)の複素共役を表しています。
一口に波動関数といっても何の波動関数を表すのかは様々ですが、例えば\phi^*(x)が電子の波動関数とすると、\rhoは電子密度を意味します。
もしも、波動関数が空間的に小さな領域に集中(局在)しているなら、微視的には粒子が確率的に存在していても、より大きいスケールの視点ではまるで一つの粒のように見えます。そういった意味で確率解釈は粒子性と波動性の両方をうまく取り込んだ解釈と言えるでしょう。
量子力学の波動関数が一体何を表しているのかは、専門家の間でも細かい解釈の違いがあります。
確率解釈につきましてはこれらの記事で詳しく紹介しています。
 「ある」と「ない」が一つの不思議な世界/シュレディンガーの猫とは
「ある」と「ない」が一つの不思議な世界/シュレディンガーの猫とは シュレディンガー方程式 Schrödinger equation
シュレディンガーさんが提案した状態方程式で(1)式や(2)式のように表されます。
\begin{equation}
i\hbar\frac{\partial \phi(\boldsymbol r,t)}{\partial t}=\mathcal{H}\phi(\boldsymbol r.t)
\end{equation}\begin{equation}
\mathcal{H}\phi(\boldsymbol r) =E\phi(\boldsymbol r)
\end{equation}(1)式を「時間依存シュレディンガー方程式」、(2)式を「時間に依存しないシュレディンガー方程式」といいます。
必ずしもそうではありませんが、波動関数の時間変化を見たい時は(1)式、ある波動関数の持つエネルギーを見たい時は(2)式といった使い方がされます。
(1)式の右辺にあるEはエネルギーの次元を持ち、エネルギー固有値 energy eigenvaluesとよばれます。
\mathcal{H}はハミルトニアン Hamiltonianといって、考えている粒子や波動のエネルギーを足し合わせた式です。中身は(3)式のように運動エネルギーとポテンシャルエネルギーの和で表されます。ポテンシャルエネルギーとは位置エネルギーのことです。
\begin{equation}
\mathcal{H}=\frac{\boldsymbol p^{2}} {2m}+V=-\frac{\hbar^{2}}{2m}\Delta+V
\end{equation}シュレディンガー方程式は拡散方程式と呼ばれる微分方程式の形をしており、量子力学的現象をうまく記述することができます。
いくつかの方法でこれらの式の妥当性を証明することができますが、そもそもなぜこの式が成り立つのかについてはよくわかっていません。
注意点として、\mathcal{H}=Eと書いてはいけません。
量子力学では、ハミルトニアンは波動関数に何らかの数学的な操作を加える「演算子」として考えます。演算子を波動関数に作用させると、それによって波動関数から係数として何らかの値が出力されたり、波動関数自体の形が変化します。
前節で説明した波動関数と、波動関数に作用する演算子という二つの概念を方程式に落とし込むことで、ニュートン力学では考えられなかった量子的な効果を導き出すことができます。
逆に、演算子と波動関数を導入しないとニュートン力学と結果が等しくなって量子的な解が得られなくなります。
また、(3)式は運動量\boldsymbol pの項がラプラシアンで書かれた形に変わっていますが、こちらもニュートン力学では考えられない式変形です。
行列形式のシュレディンガー方程式
シュレディンガー方程式は式変形によって解析的 analyticalに解くほかに、代数的 algebraicな行列計算によっても解くことができます。
この時、シュレディンガー方程式は次のような行列の式になります。
\begin{equation}
\begin{pmatrix}
\mathcal{H_{11}} & \mathcal{H_{12}} \\
\mathcal{H_{21}} & \mathcal{H_{22}} \\
\end{pmatrix}
\begin{pmatrix}
\phi_1 \\
\phi_2\\
\end{pmatrix}
=
\begin{pmatrix}
E&0\\
0&E\\
\end{pmatrix}
\begin{pmatrix}
\phi_1 \\
\phi_2\\
\end{pmatrix}
\end{equation}(5)式は線形代数の固有値方程式 characteristic equationの形をしています。
解析的には微分方程式ですが、代数的には固有値方程式の形をしているのが、シュレディンガー方程式の大きな特徴です。
式の意味を簡単に説明します。
(2)式の関数を使ったシュレディンガー方程式と(5)式を比較すると、ハミルトニアンが行列に、波動関数はベクトルの形に、エネルギー固有値は対角行列にそれぞれ変化します。
数学的に行列 matrixは、何らかのベクトルを別のベクトルに変換する操作をします。
一方、(5)式では左辺でハミルトニアンを波動関数に作用させて波動関数を変換させても、右辺で波動関数は変化していません。代わりにハミルトニアンが固有エネルギーに変化しています。言い換えると、波動関数にハミルトニアンを入力した結果、エネルギー固有値が出力結果として得られたということを表しているのです。
(5)式の各項の関係が量子力学と何の関係があるのかというと、ある波動関数のエネルギーを見ようと観測するということが、方程式上では左辺の波動関数にハミルトニアンを作用させることと対応しています。
そして、ある波動関数に対応するエネルギーがEとして観測されたということが、右辺と対応しています。
物理的には上のような対応関係がありますが、数式は単なる固有値方程式なので、エネルギーを求めるためには下に書いたような行列式を計算して固有値と固有ベクトルを求めることが、シュレディンガー方程式を解くことに相当します。
\begin{equation}
\begin{vmatrix}
\mathcal{H_{11}}-E & \mathcal{H_{12}} \\
\mathcal{H_{21}} & \mathcal{H_{22}} -E \\
\end{vmatrix}
=0
\end{equation}ちなみに、(6)式を永年方程式 secular equationと呼ぶことがあります。
シュレディンガー方程式では(6)式を解いて得られた固有値のことを、固有エネルギーまたはエネルギー固有値、固有ベクトルを固有状態 eigenstateと呼びます。
代数的にはシュレディンガー方程式のエネルギーとは、固有値方程式を解いて得られる固有値のことを指すので、関数のシュレディンガー方程式でも代数版の呼び方と同じくEをエネルギー固有値と呼称します。
このように量子力学の大きな特徴として、解析と代数の両方で互いに等価な解法が存在します。
特に、代数的な解法は数値計算と非常に相性が良いことで知られています。
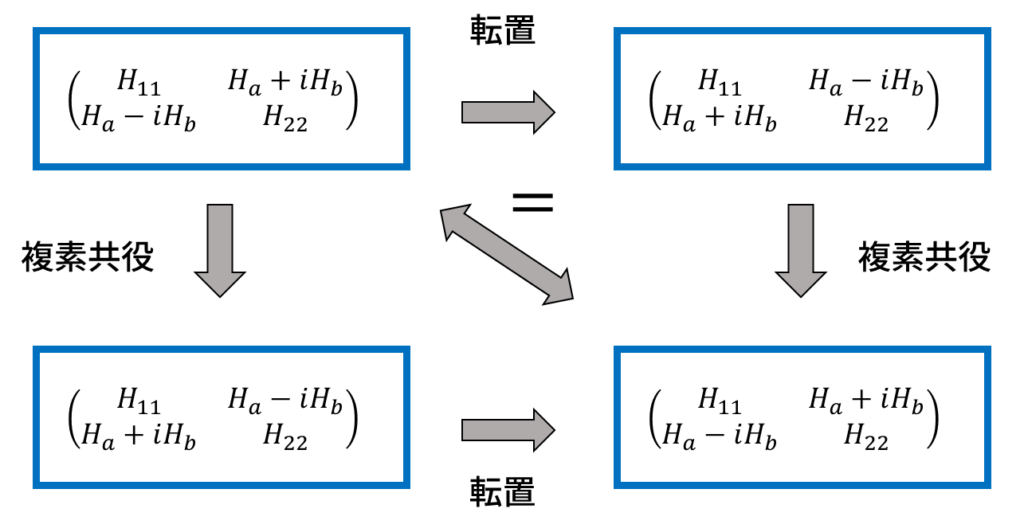
エルミート行列 Hermitean matrix
ハミルトン行列はエルミート行列 hermitian matrixと呼ばれる行列でなければなりません。
エルミート行列とは「複素転置行列が元の行列と等しくなるような行列」です。
\begin{equation}
H=H^\dagger=\begin{pmatrix}
\mathcal{H_{11}} & \mathcal{H_{a}+iH_b} \\
\mathcal{H_{a}-iH_b} & \mathcal{H_{22}} \\
\end{pmatrix}
\end{equation}H^\daggerの肩に乗っている記号はダガー daggerといい「複素共役を掛けて転置する」という意味です。
演算子 Operator
量子力学では前述で説明したハミルトニアンを演算子 operatorとみなす見方があります。普通、演算子と言えば四則演算子が思い浮かぶかと思いますが、量子力学で扱う演算子はどちらかというと微分演算子やナブラ演算子に近いです。
演算子を作用させることは波動関数に対する何らかの操作を表しています。例えば下の式を例にしましょう。
\begin{equation}
\frac{d}{dx}e^{ax}=ae^{ax}
\end{equation}(8)式はe^{ax}を微分した結果、元のe^{ax}の係数にaが掛かっています。見方を変えると、関数に演算子を作用させる(入力する)ことで、aという値が出力結果として得られたように見えます。
今度はシュレディンガー方程式に対しても同じような見方をします。ハミルトニアンを\hat{\mathcal{H}}(エイチハット)という演算子であるとすると、(2)式は「波動関数にハミルトン演算子を作用させた結果、エネルギーが出力された」ように見えます。このとき、演算の前後で波動関数は変化しません。
このような操作は特定の別の演算子でも行うことができ、ハミルトン演算子のほかにもさまざまな種類が存在します。
例えばある状態の運動量や位置を求めたいときは、数式上では波動関数に運動量演算子や位置演算子という演算子を作用させることで表します。
このように、シュレディンガー方程式は演算子や行列によって状態(波動関数)を変化させたり、物理量などの情報を取り出すことができます。
ハミルトニアンの行列はエルミート行列であることが必須でしたが、演算子も同様にエルミート演算子と呼ばれる演算子でなくてはなりません。
オブザーバブル Observable
特定の演算子が持つ「観測量(長さ、時間、エネルギーなど)を取り出せる」性質をオブザーバブル observableといいます。
私たちは波動関数を直接観測することはできず、実験によって物理量を「観測・測定」して状態を求めます。実験による物理量の測定は、数式では波動関数にオブザーバブルな演算子を作用させることで表現します。
物理量は観測可能な実数なので、オブザーバブルな演算子には「作用させると実数が取り出せる」という条件が掛かってきます。その条件とは、演算子がエルミート演算子という演算子であることです。
交換関係 Commutation relations
行列計算では二つの行列のどちらを先にかけるかで、結果が変わることがありましたね。
同様に演算子も二つの演算子を入れ替えると結果が変わることがあります。
演算子の入れ替えに関して値がどのように変化するかを示した関係を交換関係と言います。
交換関係は二つの演算子\hat{A}, \hat{B}に対して次の計算をして確かめます。
\begin{equation}
[\hat{A},\hat{B}]=\hat{A}\hat{B}-\hat{B}\hat{A}
\end{equation}(9)式の左辺は交換子 commutator、あるいはポアソン括弧式 Poisson bracketなどといい、互いに演算子を入れ替えて差をとる操作を行います。
もし(9)式の結果が0なら「交換関係が成り立つ」あるいは「可換である」といい、演算子は自由に入れ替え可能です。しかし0でなければ演算子の入れ替えで得られる結果が変わります。
交換関係が成り立つ場合、二つの演算子に対して状態は一つに決まり同時固有状態 simultaneous eigenstatesをもつ」といいます。
それぞれの演算子がオブザーバブルかつ可換なら、二つの物理量は同時に観測することができます。
逆に可換でなければ、演算子のどちらかを先に作用させるかで状態が変わってしまうので、実験でも同じ状態に対して二つの物理量を同時に計測することはできません。
交換関係は不確定性原理の説明にも用いられます。
ハイゼンベルグの不確定性原理 Heisenberg uncertainty principle
位置と運動量を高精度に同時には求められないという原理です。
運動量を速度とした書籍やもありますが、確率解釈で説明したように粒子は確率的に存在します。そのため確率的に存在する粒子に対して速度は定義されないため、運動量で書く方が正確です。
逆に速度が定義されない確率的な粒子にも、運動量に相当する何かが存在するともいえます。
交換子で表現すると次の通りです。
\begin{equation}
[\hat{x},\hat{p}]=i\hbar
\end{equation}(10)式は可換ではなく、同時固有状態を持ちません。したがって位置と運動量を同時に計測することができず、不確定性原理を満足します。
今回の記事は以上になります。
ご覧いただきありがとうございました。
少しでも興味がある方は、他の記事も読んでいただければ幸いです。さらに量子力学の理解度が深まるはずです。
当サイトで取り上げた記事のほか、Twitter でもさまざまな情報を発信していますのでよろしければフォローをお願いします。
マサ: @masa_fpp03