15分でわかる暗算法【Trachtenberg systemからインド式計算まで】

当たり前にスマホが普及した令和を生きる私たちが暗算法を勉強する理由・利点はなんでしょうか？
私は「スマホを取り出すより速く計算できる」ことと「スマホがない状況でもとりあえず計算できるようになる」ことだと思います。

義務教育で習う”筆算”は一昔前では理に適った計算方法でしたが、どんな人間よりも速く正確に計算できるスマホが紙とペンよりも身近にある現代には適していません。もし「スマホがない」状況を想定するなら「紙もペンもない」と考えるのが自然です。

そして、それこそが筆算の最大の難点なのですが、殆どの人は「紙とペンがないと計算しようと思わなくなる」ことでしょう。友人に6×8は？と聞かれた時に48と答えることができても、16×8は？と聞かれたらスマホを取り出す人も多いのではないでしょうか？

筆算ばかり教えないで、こういう「16×8は2×8×8=2×64に変換すれば簡単に計算できる」とか「掛け算は前の桁から掛ける」ということも教えるべきです。
本記事では、そのような暗算をする際に使える「計算の精度を落とさずに計算プロセスを簡略化する方法」をまとめました。

Contents SHOW

肩慣らし: 数字を素早く読む

一万を超える数を読み上げる時に右の桁から「一、十、百、千、万、十万、百万…」と数えていませんか？

そういう方は、数字の間に書かれている,(コンマ/カンマ、comma)を活用しましょう。
このコンマは数字を3桁ごとに区切るので、千(1,000)や百万(1,000,000)といった位取りの目安になります。

日本の数字は4桁ごとに桁の名前が変わるのに(万→億→兆)、なぜ3桁ごとに数字を区切るか。それは海外の数字は3桁ごとに名前が変わるからです。

コンマ付き数字English 🇬🇧🇺🇸日本語 🇯🇵10^n
1one一10^0
10ten十10^1
100hundred百10^2
1,000thousand千10^3
10,000ten thousand万10^4
100,000hundred thousand十万10^5
1,000,000million百万10^6
10,000,000ten milion千万10^7
100,000,000hundred million億10^8
1,000,000,000bilion十億10^9
………
1,000,000,000,000trilion兆10^{12}

とりあえずは千、百万、十億の桁のすぐ右下にはコンマがあることだけでも覚えましょう。
慣れてきたら100,000は千より2桁大きい(百万より一桁小さい)数だから十万とわかるようになります。

「日本の数字は4桁ずつ名前が変わり、英語では3桁ずつ変わっていること」を理解しているだけでも副次的効果として以下のような計算がよりわかりやすくなります。

  • 一万×一万=一億
    10^4 \times 10^4 = 10^8
  • 一万×一億=兆
    10^4 \times 10^8 = 10^{12}
  • 千 thousand ×千 thousand =百万 million
    10^3 \times 10^3 = 10^6
  • 百万×千=十億 billion
    10^6 \times 10^3 = 10^9
  • 百万×百万=兆 trillion
    10^6 \times 10^6 = 10^{12}

掛け算と割り算のTips

2桁×2桁の王道: Trachtenberg systemlate

2桁×2桁の決定版とも言える超万能計算方法です。
この方法はGiftedという映画でも紹介されており、一度は聞いた方がいるかもしれません。
仰々しい名前の通り、Tretchtenberg System (wiki) ではたくさんの暗算方法が体系を成していますが 、2桁×2桁に限定した際の方法はとても簡単です。

式で表しても簡単なのですが、具体的に計算プロセスが想像できるように図を添付しました。

(10a + b)(10c + d) = 100ac + 10(ad + bc) + bd

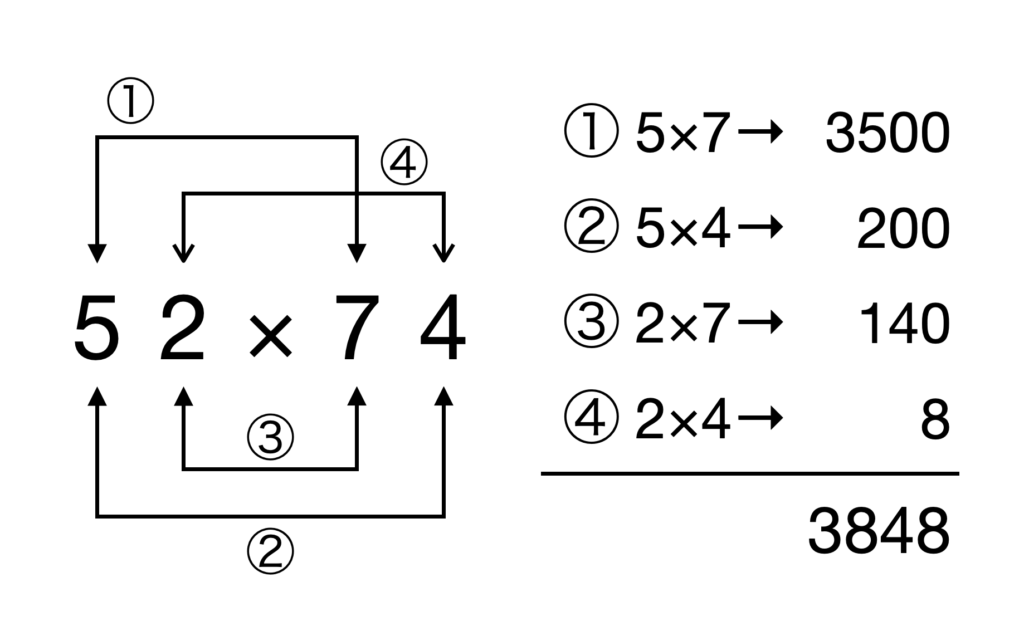
計算順序を忘れそうだという方はFOIL「First, Outer, Inner, Last」と覚えましょう。

Trechtenberg System の大きな特徴は「上の桁(大きい数)から計算すること」と「100の桁(②と③の結果)を先に足すこと」です。
筆算に慣れてしまっている人は初めのうちは上の桁から計算することに不自由を感じるかもしれません。計算途中に繰り上がりが起きて、前の計算結果を脳内で修正しないといけないのが面倒に感じると思います。
しかし、そのように何度も前に計算した数字を使いながら計算していくため、最後まで計算し切った時でも全ての数を覚えていられるようになります。筆算は良くも悪くも一つひとつの計算結果が独立してしまっているのです。

3桁×2桁もやってみよう

2桁×2桁より手間が倍くらいかかりそうだと感じるかもしれませんが、問題の見方次第ではとても簡単になります。具体的に言うと、135×57を100×57と35×57に分割するだけです。

\begin{aligned}
135 \times 57 &= 100 \times 57 + 35 \times 57 \\
& = 5700 + 1500 + 10(21 + 25) + 35 \\
& = 7200 + 495 \\
& = 7695
\end{aligned}

練習問題

  1. 36×27
  2. 44×44
  3. 298×18
  1. 972
    • 100(2×3) + 10(3×7+6×2) + 6×7 = 600+330+42
  2. 1,936
    • 100(4×4) + 10(4×4+4×4) + 4×4 = 1,600+320+16
  3. 5,364
    • (200×18) + 98×18 = 3,600+900+800+64

(a+b)(a-b)

(a+b)(a-b) = a^2 – b^2になることを大半の人は学んだはずですが、実際に使えている人はどれほどいるでしょうか？せっかくなのでここで練習しましょう。

  1. 29×31
  2. 85×75
  3. 47×41
  1. 899
    • (30-1)(30+1) = 30^2 – 1^2 = 900 – 1
  2. 6,375
    • (80+5)(80-5) = 80^2 – 5^2 = 6,400 – 25
  3. 1927
    • 44^2 – 3^2 = (1600 + 320 + 16) – 9

×25, ÷25

25を掛けることは少ないかもしれないですが、÷25は0.04%を計算するとき(次節参照)などに使うので頭の片隅にはおいておきましょう。

×25

×25は\times \frac{100}{4}と脳内変換します(÷4と×100は順不同)。

\begin{aligned}
12,345,678 \times 25 &= 12,345,678 \div 4 \times 100 \\
&=3,086,419.5 \times 100 \\
&=308,641,950
\end{aligned}

÷25

÷25は\times \frac{4}{100}と脳内変換します(÷100と×4は順不同)。

\begin{aligned}
98,765 \div 25 &= 98,765 \times 4 \div 100 \\
&=395,060 \div 100 \\
&=3,950.6 \\
\end{aligned}

同じように、×5 を\times \frac{10}{2}に変換したり、÷5を\times \frac{2}{10}を変換することもできます。僕は普通に掛けたり割ったりしますが、偶数×5の場合は248×5=(124×2)×5=124×10のように変換することもあります(やってることは分数にした時と同じです)。好みに応じて使ってみてください。

小数点と分数の便利な変換表

小数の掛け算や割り算は分数に直して計算する方が楽なことが多いです。例えば、2975の0.04%を計算するときは4を掛けてから100で割るよりも初めから「25で割る」方が楽そうですよね？

0.05の倍数

  • 0.05 = \frac{1}{20}
  • 0.15 = \frac{3}{20}
  • 0.35 = \frac{7}{20}
  • 0.45 = \frac{9}{20}
  • 0.55 = \frac{11}{20}
  • 0.65 = \frac{13}{20}
  • 0.85 = \frac{17}{20}
  • 0.95 = \frac{19}{20}

0.2の倍数

  • 0.2 = \frac{1}{5}
  • 0.4 = \frac{2}{5}
  • 0.6 = \frac{3}{5}
  • 0.8 = \frac{4}{5}

0.25の倍数

  • 0.25 = \frac{1}{4}
  • 0.5 = \frac{1}{2}
  • 0.75 = \frac{3}{4}

その他

小数分数倍数
0.008\frac{1}{125}\frac{2}{125} = 0.016, \\ \frac{3}{125} = 0.024, \\ \frac{4}{125} = 0.032
0.01\frac{1}{100}
0.02\frac{1}{50}\frac{3}{50} = 0.06, \\ \frac{7}{50} = 0.14,\\ \frac{9}{50} = 0.18
0.04\frac{1}{25}\frac{2}{25} = 0.08, \\ \frac{3}{25} = 0.12, \\ \frac{4}{25} = 0.16
0.05\frac{1}{20}
0.1\frac{1}{10}
0.125\frac{1}{8}\frac{3}{8} = 0.375, \\ \frac{5}{8} = 0.625, \\ \frac{7}{8} = 0.875
0.2\frac{1}{5}
0.25\frac{1}{4}
0.5\frac{1}{2}

もちろん、480の0.04%を計算するときは4.8×4の方が簡単なので、一概に分数に直せば全ての計算が簡略化できるとは言いません。

公約数を見つけよう

個人的に、日々の生活の中では掛け算よりも分数を約分する(cross-reducing, simplifing, canceling)ことが多い気ので、公約数 common factors の見つけ方をまとめます。

Euclidean Algorithm ユークリッドの互除法

ユークリッドの互除法ごじょほう(Euclidean algorithm, Euclid’s algorithm)とは、2つの整数の最大公約数 Greatest Common Divisor (GCD) [1]最大公約数をGreatest Common Factor: GCF と言うこともありますを求める計算法です。

具体的なステップは以下のようになります。

  1. 大きい数を割られる数 numerator とし、小さい数を割る数 denominator とする
  2. numerator ÷ denominatorの余りremainder を求める
  3. 小さい数をnumerator とし、余りをdenominator とする
  4. 余りが0になるまで2と3のステップを繰り返す
  5. 余りが0になった時のdenominator が最大公約数
\begin{aligned}
391 \div 238 &= 1R153 \\
238 \div 153 &= 1R85 \\
153 \div 85 &= 1R68 \\
85 \div 68 &= 1R17 \\
68 \div 17 &= 4(R0) \\
\therefore \gcd(391, 238) &=17
\end{aligned}

暗算で上記のような数ステップをやるのは時間と労力を消費しますよね。
なので、計算途中で余りに約数を見つけたらそこで切り上げることも可能です。
上記の例で言えば、余りが85と出た時点で17×5だとわかったらそこで計算をやめてもいいですし、153が17×9だと知っていればそこでやめても構いません。

倍数の判別方法

「この数は◯で割れそうだ」という感覚は日頃から数字に触れていないと難しいですが、その数字が2で割れるか、3で割れるか、5で割れるかを簡単に判別する方法があります。

  • 2の倍数→最後の桁が2で割り切れるか
    • 4の倍数→最後の2桁が4で割り切れるか
  • 5の倍数→最後の桁が5で割り切れるか
    • 25の倍数→最後の2桁が25で割り切れるか
  • 3の倍数→全ての桁の数の和が3で割り切れるか
    • 9の倍数→全ての桁の数の和が9で割り切れるか

3.14よりも正確な\piの計算

みなさんは22/7(ナナブンノニジュウニ)というアイドルを知っていますか？(唐突)
天城あまきサリーちゃんや川瀬詩かわせうたちゃん、涼花萌すずはなもえちゃんは可愛すぎて眼福です。(困惑)
女優の浅倉唯あさくらゆいさんも以前は加入していたんですよ。(呆然)

アイドルグループの話はさておき、\frac{22}{7}という数字は\piの値に近似しており、3.14よりも正確な値に近いことが知られています。

\begin{aligned}
\pi &= 3.141592... \\
\frac{22}{7} &= 3.142857... \\
|\pi - \frac{22}{7}| &= 0.001265... \\
|\pi - 3.14| &= 0.001592...
\end{aligned}

なので、半径が7の倍数の円や球の面積/体積を求める場合は\pi \fallingdotseq \frac{22}{7}として計算しましょう。

もっと正確な方がいいと言う方は(いつ使えるかはわかりませんが)\pi \fallingdotseq \frac{355}{113}としてもいいです。分数の左下から見て113355と覚えましょう(間違っても暗証番号にはしないように)。\piとの差分は驚異の0.0000002667…です。

インド式掛け算6選

インド式掛け算 Vedic Mathematics とは、掛け算や累乗、累乗根などを簡単に計算できる16種類の式をまとめたものです。発案者はインド人のJagadguru Shri Bharathi Krishna Tirthaji で、20世紀に出版されたVedic Mathematics Book by Tirthaji Maharaj によって世間から知られるようになります。
Vedic とはサンスクリット語で「知的な」という意味なので、Vedic Mathematics を直訳すると「知的な計算法」となります。

×11

×11は、掛ける相手が2桁だろうが3桁だろうが、それこそ100桁だろうが共通の法則があります。
それは「掛ける相手の数を二つイメージして、その一つを10倍してから足す」です。

69×11=759

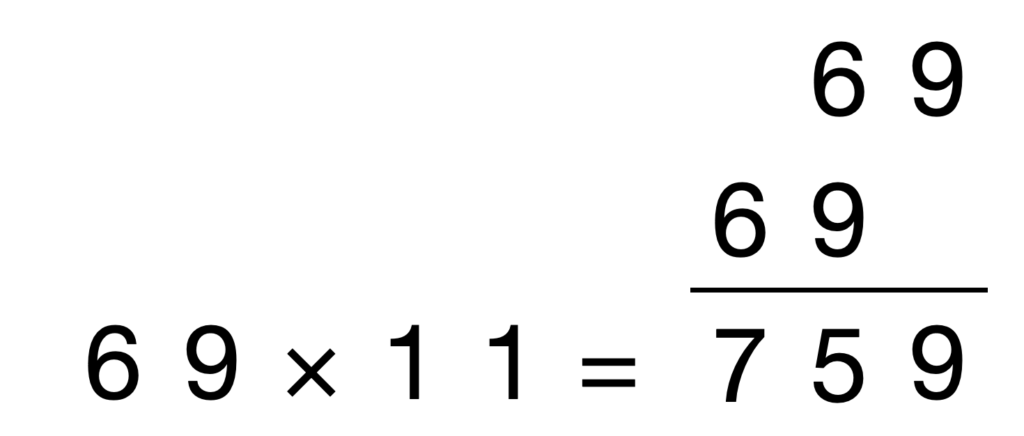
なぜ上記の方法で計算できるかと言うと、11は(10+1)に分解でき、分配法則によりa×(10+1)を10a + aと計算できるためです。その法則は2桁×11でも3桁×11でも成り立ちます。

\begin{aligned}
(10a + b) \times (10 +1) &= 100a + 10a + 10b + b \\
&= 100a + 10(a + b) + b
\end{aligned}
\begin{aligned}
(100a + 10b + c) \times (10 + 1) &= 1000a + 100b + 10c + 100a + 10b + c \\
&= 1000a + 100(a + b) + 10(b + c) + c
\end{aligned}

2桁×99

×99をする際は、掛ける数字から1を引いた数(＊)を100倍したものと、99から＊を引いた数の和で計算できます。視覚的に解くなら以下のようになります。

57×99=5,643
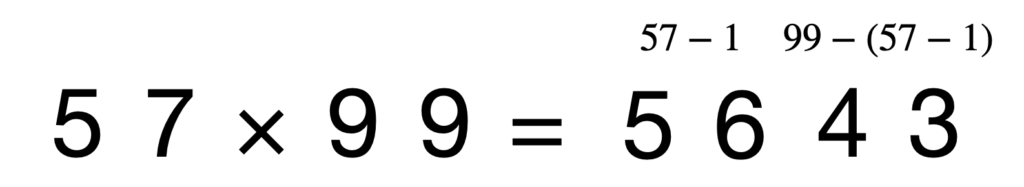
\begin{aligned}
(10a &+ b) \times 99 = 990a + 99b \\
&= (1000a - 10a + 100b - 1b) + (-100+100) \\
&= (1000a + 100b -100) - 10a - 1b + 100 \\
&= 100(10a+b-1) + (100-(10a+ b)) \\
&=100(10a+b-1) + (99-(10a+b-1))
\end{aligned}

100から引き算するより、99から「予め1を引いた数」で引き算した方が繰り下がりがなくなるため、わざわざ(99-(10a+b-1))と変形しています。同じテクニックを下の「¥10,000からのおつりの計算」でも解説しています。

2桁×2桁: 一の位の数が同じで十の位の和が10

1◯×9◯, 2◯×8◯, 3◯×7◯, 4◯×6◯, 5◯×5◯の、◯に同じ数が入るような場合に使える暗算法があります。

43×63=2,709

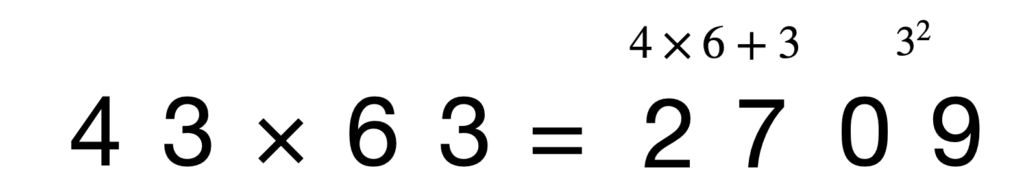
例え◯に入る数が9でも9^2=81と100以下であるため、初めに100倍した数との足し算が発生しません。

\begin{aligned}
a + b &\equiv 10 \\
(10a + c) \times (10b + c) &= 100ab + 10ac + 10bc + c^2 \\
&= 100ab + 10c(a + b) + c^2 \\
&= 100ab + 100c + c^2 \\
&= 100(ab + c) + c^2
\end{aligned}

2桁×2桁: 十の位の数が同じで一の位の和が10

◯1×◯9, ◯2×◯8, ◯3×◯7, ◯4×◯6, ◯5×◯5の、◯に同じ数が入るような場合に使える暗算法もあります。

74×76=5,624

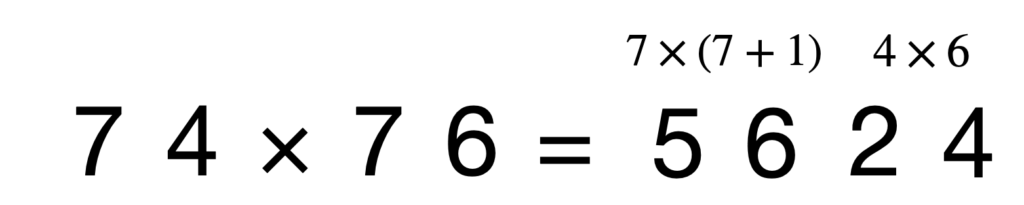
(75-1)(75+1)=75^2-1としてもいいですが、結局75×75は「一の位が同じで十の位の和が10」なので初めからこちらの方法を使った方が楽です。

\begin{aligned}
b + c &\equiv 10 \\
(10a + b) \times (10a + c) &= 100a^2 + 10ab + 10ac + bc \\
&= 100a^2 + 10a(b + c) + bc \\
&= 100a^2 + 100a + bc \\
&= 100a(a + 1) + bc
\end{aligned}

2桁×2桁: 11~19×11~19

17×13=2,021

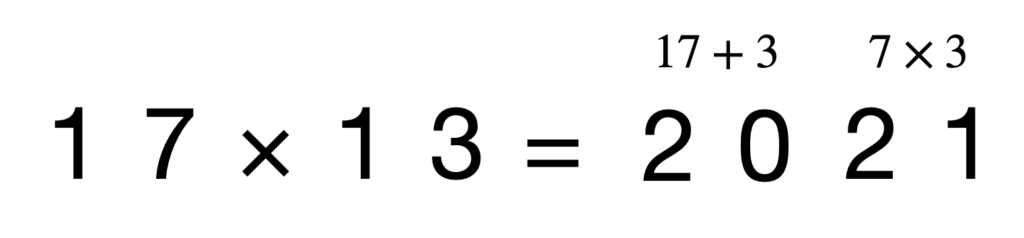
こんな暗算法もあるので証明は下に書きましたが、九九を覚えられる人間ならもう81個の掛け算くらい暗記してもいいかもしれませんね。
19までの掛け算表は本記事の最後の方にまとめてあります。

\begin{aligned}
(10 + a) \times (10 + b) &= 100 + 10a + 10b + ab \\
&= 100 + 10(a + b) + ab \\
&= 10(10 + a + b) + ab
\end{aligned}

2桁の3乗

「2桁の3乗なんて練習してどうすんだ」って？結論から言えば「凄い人感」を出せる！
なぜなら、2桁×2桁を暗算できたとしてもスマホで検算された挙句「〇〇さん、計算早いですね」くらいしか言われませんが、2桁の3乗を計算できると「天才じゃないですか！」と言ってもらえます(多分)。
最悪、豚箱にぶち込まれた時の暇つぶしになります。

とは言え、さすがに今回は紙とペンを使わないと難しいと思いますので興味のある方はご覧ください。
原理的には以下の式と、2つの鍵となる考え方を基に計算します。

(10a+b)^3 = 1000a^3 + 100(3a^2b) + 10(3ab^2) + b^3
  • 3a^2bをa^2b+2a^2bと計算する
  • 各桁毎にa^3, a^2b, ab^2, b^3と別々に考えるのではなく、左端のa^3 に\times \frac{b}{a}しながら計算する

今回は、比較的簡単に計算できる以下の3パターンを図示します。

17^3 = 4,913
71^3 = 357,911
77^3 = 456,533

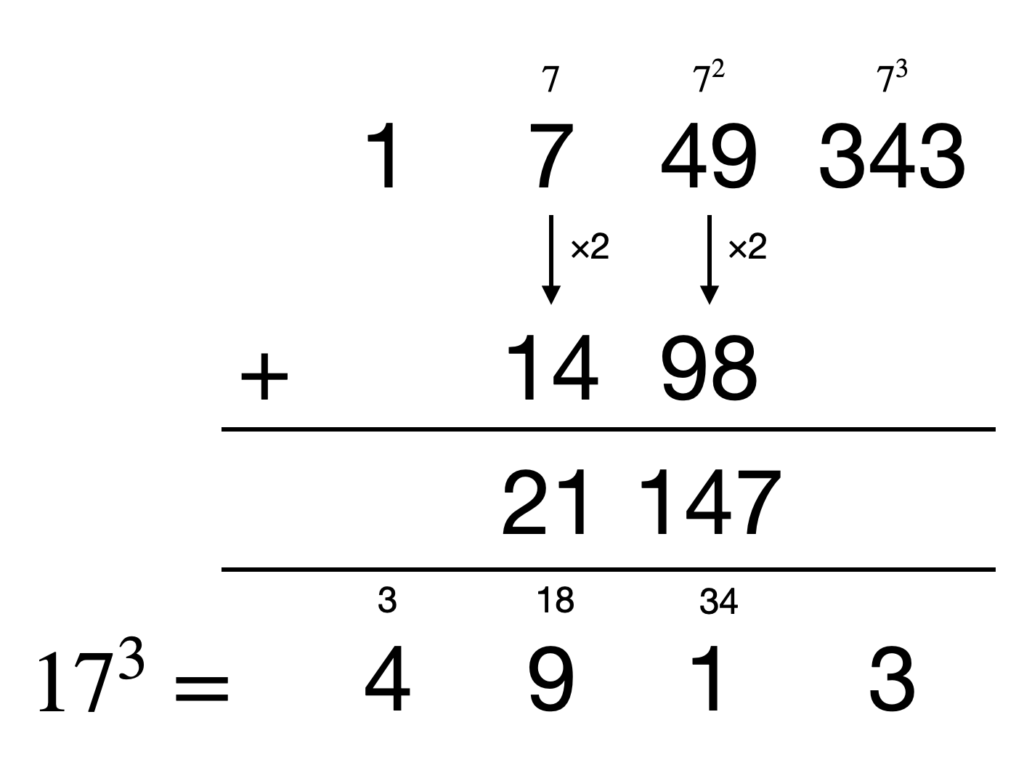
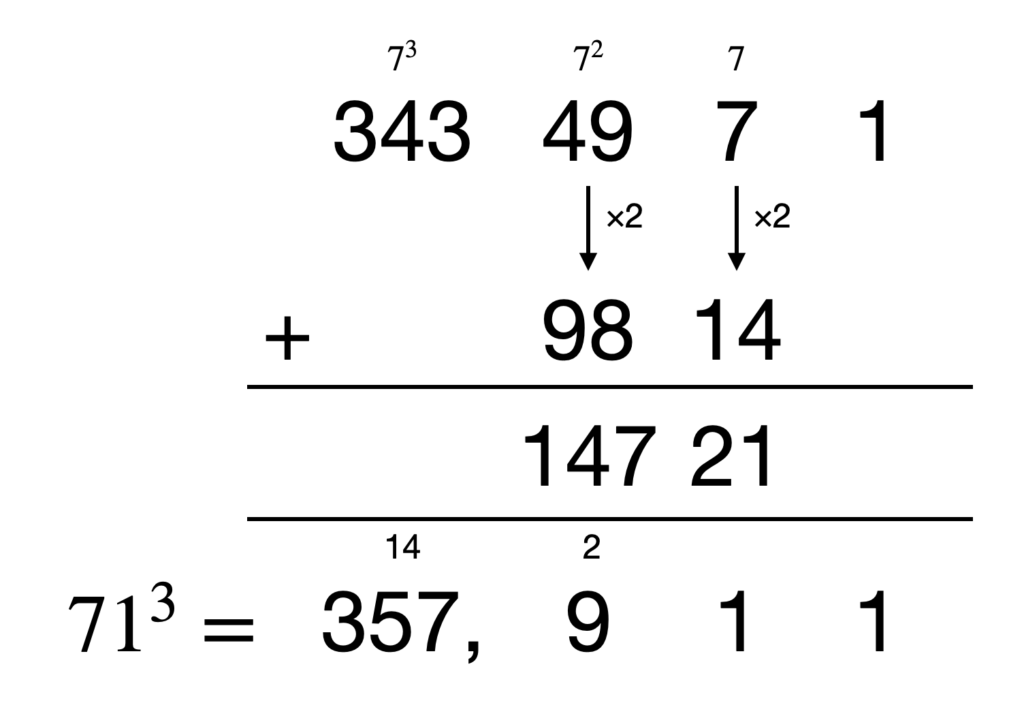
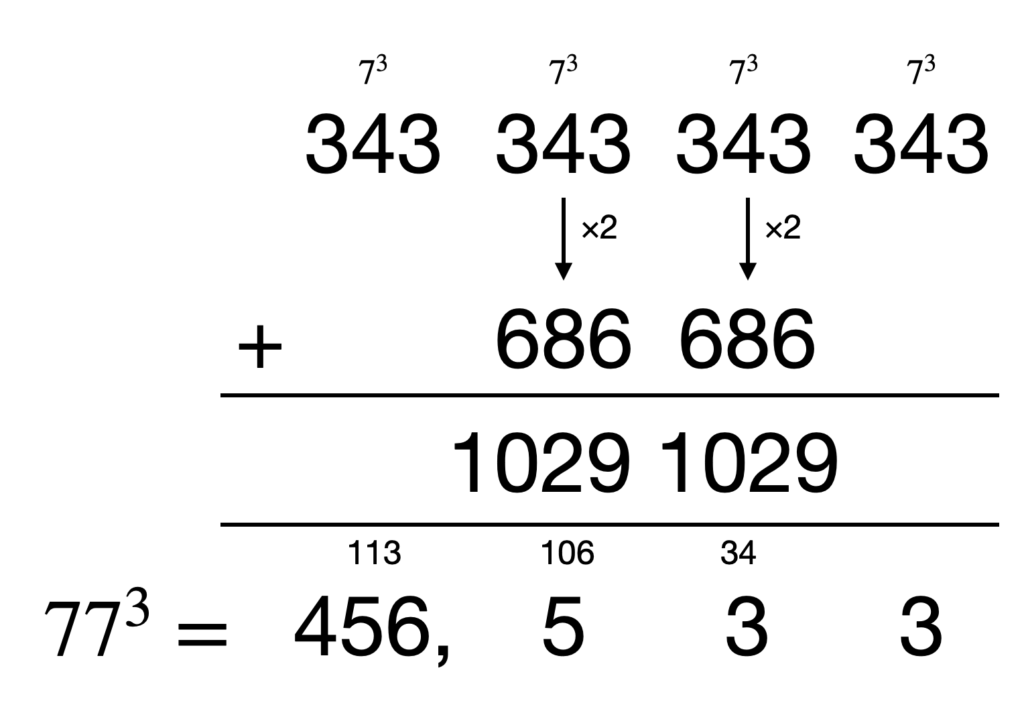
足し算・引き算のTips

足し算と引き算に役立ちそうな簡略化の方法はあまり多くありません。つまり、練習だけが計算の精度と速度を向上します。

しかし、一般的に言われる「和が10になるように項をまとめよう」とか「298は300として概算しよう」みたいな話にうんざりしている人のために、使用場面は限られているけど忘れがちな計算の簡略化を3つ紹介します。

等差数列型

大層な名前が付いていますがなんてことはありません。「各項が同じような値に分布していたらまとめて足してしまおう」と言う作戦です。

\begin{aligned}
17+ 20 &+ 24 + 18 + 19 + 21 + 23\\
&= 17 + 18 + 19 + 20 + 21 + (22 + 2) + 23\\
&= 7 \times \frac{17+23}{2} + 2 \\
&= 7 \times \frac{40}{2} + 2\\
&= 7 \times 20 + 2 \\
&= 142
\end{aligned}

念の為、等差数列の和を求める公式も紹介します。

初項から末項までの等差数列の和

\begin{aligned}
S = n \frac{a+L}{2}
\end{aligned}
  • S: 等差数列の和 Sum of Arithmetic Sequence/Series
  • n: 項の数 number of terms
  • a: 初項 first term [2]日本では初項をa_{0}と書くことが多いです
  • L: 末項 last term [3]日本では末項をa_{n}と書くことが多いです

初項から末項の1つ前までの等差数列の和

\begin{aligned}
S = n \frac{2a + (n-1)d}{2}
\end{aligned}
  • d: 公差 common difference

等比数列型

学校で習ったけど結局使えない公式No. 1の等比数列の総和の式を練習してみましょう。

公比が1より大きい等比数列の和

\begin{aligned}
S = a \frac{r^n - 1}{r-1}
\end{aligned}
  • S: 等比数列の和 Sum of Geometric Sequence/Series
  • n: 項の数 number of terms
  • a: 初項 first term
  • r: 公比 common ratio

公比が1より小さい等比数列の和

\begin{aligned}
S = a \frac{1-r^n}{1-r}
\end{aligned}

練習問題

あえて簡単な問題にしましたが、グループにせずに等比数列の和の公式を試してみてください。

  • 3 + 6 + 12 + 24 + 48 + 96
  • 7 + 21 + 63 + 189
  • 27 + 18 + 12 + 8
  • 129
    3 \frac{2^6-1}{2-1} = 3 \times 63
  • 280
    7 \frac{3^4-1}{3-1} = 7 \times 40
  • 65
    27 \frac{1-\frac{2}{3}^4}{1-\frac{2}{3}} = 27 \frac{\frac{65}{81}}{\frac{1}{3}} = 27\frac{65}{27}

¥10,000札からのお釣り

引き算で一番ミスしやすい箇所は繰り下がりです。その典型例が一万円札や五千円札からのお釣り計算でしょう。したがって、引き算でミスを少なくするためには計算中の繰り下がりの回数を減らすことが最も効果的です。

解決策は至って簡単。黙ってSuicaかPayPayかクレジットカード使え。10,000から数字を引くのではなく、予め数字1引いた数を9,999から引きます。端数によっては予め10を引いた数を9,990から引くことも可能です。

\begin{aligned}
10,000 - 5,460 &= (9,990 + 10) - 5,460 \\
&= 9,990 - (5460 - 10) \\
&= 4540
\end{aligned}

人によっては9,999から数字を引き、最後に+1する方が楽だと感じるそうです。お好きな方を選んでください。

いっそのこと覚えると便利な掛け算の表

累乗

2の累乗

覚えていると割と便利？なものが2の累乗です。

\begin{aligned}
32 \times 64 &= 2^5 \times 2^6 \\
&= 2^{(5+6)} = 2^{11} = 2048
\end{aligned}
\begin{aligned}
16 \times 625 &= 2^4 \times 5^4 \\
&= (2 \times 5)^4 = 10,000
\end{aligned}
\[2^4\]\[2^5\]\[2^6\]\[2^7\]\[2^8\]\[2^9\]\[2^{10}\]\[2^{11}\]\[2^{12}\]\[2^{13}\]\[2^{14}\]\[2^{15}\]\[2^{16}\]
1632641282565121,0242,0484,0968,19216,38432,76865,536

3の累乗

\[3^3\]\[3^4\]\[3^5\]\[3^6\]\[3^7\]\[3^8\]\[3^9\]\[3^{10}\]
278124372921876,56119,68359,049

5の累乗

\[5^3\]\[5^4\]\[5^5\]\[5^6\]\[5^7\]\[5^8\]\[5^9\]\[5^{10}\]
1256253,12515,62578,125390,6251,953,1259,765,625

忘れた時は、×5のテクニック(\frac{10}{2})を使って計算してみましょう。

19までの掛け算と平方、立法

9×9までを覚えたら、次は19×19まで覚えちゃいましょう。意外と便利です。
私は床屋で髪を切っている間に頭の中で練習しています。(話しかけれることがないため)

×111213141516171819
2222426283032343638
3333639424548515457
4444852566064687276
5556065707580859095
6667278849096102108114
777849198105112119126133
88896104112120128136144152
999108117126135144153162171
10110120130140150160170180190
11121132143154165176187198209
12132144156168180192204216228
13143156169182195208221234247
14154168182196210224238252266
15165180195210225240255270285
16176192208224240256272288304
17187204221238255272289306323
18198216234252270288306324342
19209228247266285304323342361
x^2x^3
248
3927
41664
525125
636216
749343
864512
981729
101001000
111211331
121441728
131692197
141962744
152253375
162564096
172894913
183245832
193616859
×111213141516171819
2
33639424548515457
44852566064687276
56065707580859095
67278849096102108114
7849198105112119126133
896104112120128136144152
9108117126135144153162171
10
11121132143154165176187198209
12132144156168180192204216228
13143156169182195208221234247
14154168182196210224238252266
15165180195210225240255270285
16176192208224240256272288304
17187204221238255272289306323
18198216234252270288306324342
19209228247266285304323342361
x^2x^3
28
327
464
5125
6216
7343
8512
9729
10
111211331
121441728
131692197
141962744
152253375
162564096
172894913
183245832
193616859
×111213141516171819
2222426283032343638
333
444
555
666
777
888
999
10110120130140150160170180190
11
12
13
14
15
16
17
18
19
x^2x^3
24
39
416
525
636
749
864
981
10100
11
12
13
14
15
16
17
18
19

これで暗算法は終わりです。

実際に練習をしてみたいという人のために記事を作成中です。

参考

また、「やっぱり私はスマホで計算するから」という人のために、英語で音声アシスタント(Siri, Alexa)を使って計算する方法をまとめた記事を作成中です。

参考

Terminology

Terminology
↑1 最大公約数をGreatest Common Factor: GCF と言うこともあります
↑2 日本では初項をa_{0}と書くことが多いです
↑3 日本では末項をa_{n}と書くことが多いです

コメントを残す

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です

CAPTCHA


前の記事

macOS で使えるショートカット一覧

次の記事

「ある」と「ない」が一つの不思議な世界/シュレディンガーの猫と…