中学や高校の時に習う古典物理学 classical physicは私たちが普段住んでいるような、原子一つが全く見えないほど大きな世界を扱っています。
例えば、ニュートンの法則ではボールや振り子の運動から惑星の公転に至るまで、私たちの目に見える物体よりも大きな長さの領域に対しては、正確に速度や力を計算することができます。
しかし、原子や分子ほどの小さな世界に対してはニュートンの法則は通用しないため、新しい学問が必要になります。それが量子力学 quantum mechanicsです。
量子力学では古典物理学には登場しない波と粒子の性質をあわせ持った量子 quantumと呼ばれる単位量 unit quantityを扱います。今回はそんな量子について解説したいと思います。
Contents SHOW
量子は飛び飛びの値を持つ
量子 Quantum
古典物理学では原子一個だけの運動に注目することはありませんでした。例えば、水面の波や物質中の熱の伝搬は膨大な数の原子や電子の集団[1]大体10^{23}個程度、多すぎる!が一斉に動いていますが、理論上は一つの波動として扱います。
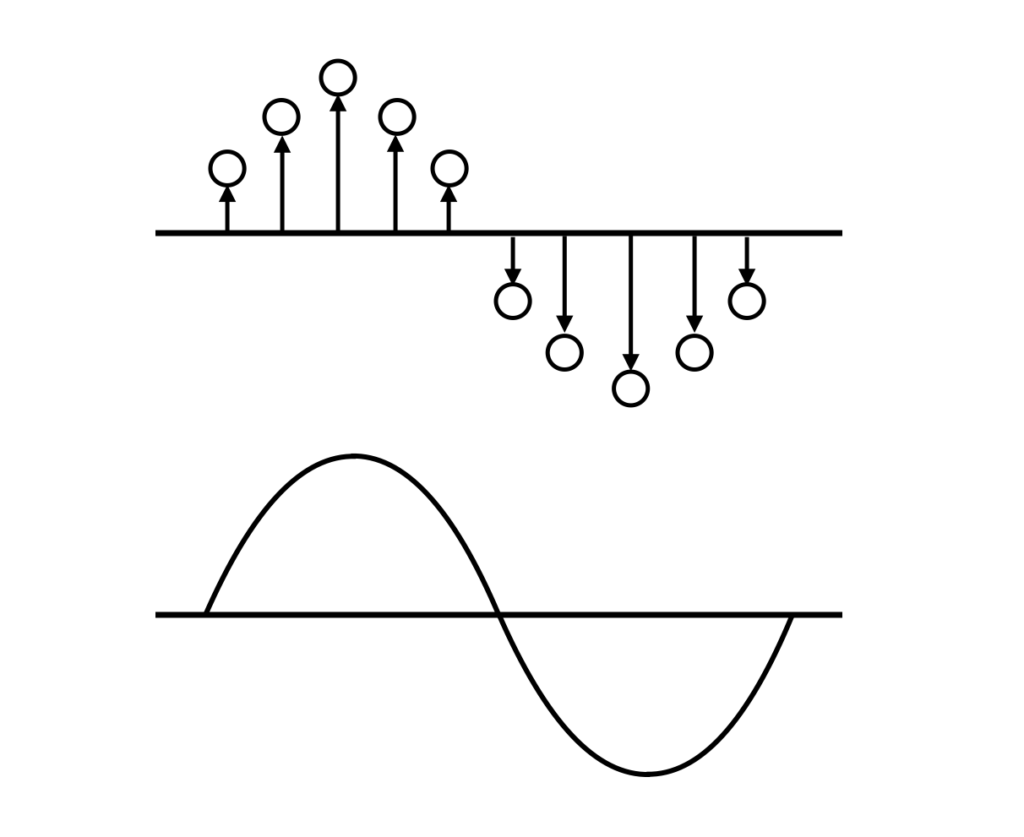
また、例えば野球ボールは、実際には多数の原子が結合することで全体として大きな塊で存在していますが、その運動を調べるときは、細かい原子の振る舞いを無視して「ボール」という一つの物体として扱います。
波と粒は古典物理学では全く違う概念であり、従う方程式も異なります。
それに対し、量子力学ではこれまで無視してきた原子一粒くらい小さな物質の運動に焦点を当てます。そこでのあらゆる現象は私たちが普段生活している世界とは根本的に違い、粒子や波動はお互いに波と粒子の性質を合わせ持ちます(波動と粒子の二重性)。この波と粒の性質を合わせ持った小さな物質やエネルギーを量子と呼びます。
量子の持つ波と粒の二重性についてはこちらの記事にまとめました。二重スリット実験を題材に別途わかりやすく紹介していますので興味のある方はご覧ください。
 波動性と粒子性とは/二重スリット実験から多世界解釈まで
波動性と粒子性とは/二重スリット実験から多世界解釈まで 量子化 Quantization
古典物理学で定義されていた粒子や波動を量子力学で扱えるように再定義することを、量子化 quantizationといいます。
量子化を行うと、古典物理学では別々に考えられてきた、粒子と波動という相反する性質を両方持つようになります。
例えば、原子の構成要素の一つである電子 electronを量子化すると、粒子に加え波の性質が現れます。逆に、光を量子化すると波の他に粒子の性質が現れます。量子化した光を光子 photonといい、光子は量子としての見方を強めた呼び方です。

量子化するかどうかは実際の現象と整合性を合わせて決定するほか、理論や計算を簡単にしたいときは選択的に決めることがあります。例えば、電子に光を照射したモデルを考えるときに、理論上では電子だけを量子化して光は量子化しないということもできます。つまり、このモデルでは、量子化されていない単純な波動としての光が、量子化された電子に当たっているという見方になります。
ただし、理論上では量子化は選択的に行われていても、現実にはどれくらい小さい世界で物質やエネルギーが量子として振る舞うのかはいまだにはっきりしていません。
離散的 Discrete
量子の最も大きな性質はエネルギーなどが飛び飛びの値をとることです。この性質を専門的には「エネルギーが離散的な値をとる」といいます。
量子力学の離散的なエネルギーを理解するためにも、まずは古典力学のエネルギーの性質を見てみましょう。一番わかりやすいのは物体の自由落下でしょうか。自由落下の運動はニュートンの運動方程式から導けます。xのマイナス方向に落下する運動を考えて、
-g [\text{m} / \text{s}^2]:重力加速度
v_0 [\text{m} / \text{s}]: 初速度
x_0 [\text{m}] : 初期位置
とすると物体の運動は下の式になります。
x=-\frac{1}{2}gt^2+v_0t+x_0 \quad [\text{m}]\begin{aligned}
& F=ma=m\dfrac{d^2 x}{d t^2} \quad [\text{N}] \quad (=[\text{kg}\cdot \text{m}/\text{s}^2]) \\[3mm]
& \frac{d^2 x}{d t^2}=\frac{F}{m}=-g \quad [\text{m} / \text{s}^2] \\[3mm]
& \frac{dx}{d t}=-gt+v_0 \quad [\text{m} / \text{s}] \\[3mm]
& x=-\frac{1}{2}gt^2+v_0t+x_0 \quad[\text{m}]
\end{aligned}初速v_0=0、初期位置x_0=30で物体の運動の軌跡を表すとこのようなグラフが書けます。

グラフを見て分かる通り物体の運動は滑らかな放物線を描きます。放物線という言葉からわかるように、自由落下のような古典力学の運動はどんなに時間の幅を細かく刻んでも、その間には必ずt やx の値が存在します。例えば、時刻0.25秒と0.26秒の間の時間には0.2500001や0.2599999…など無限に細かい数字が存在します。
このように、ある値と値の間にいくらでも細かな別の値を取ることを数学用語で連続的 continuousといいます。古典物理学では常に連続的な量を扱ってきました。今回例にした自由落下の運動以外でも、普段私たちが目にする運動は連続した軌跡を描きます。
しかし、量子力学は離散的な振る舞いをする量子を扱います。連続的な振る舞いをする古典力学と離散的な量子力学の間にある違いは一体なんでしょうか?
その答えは、見ているエネルギーの大きさの違いにあります。古典力学ではエネルギーは数ジュールや数百ジュールといった世界を扱うのに対し量子力学の見ているエネルギーは非常に小さいです。
量子が見ているエネルギーがどれだけ小さいのかを理解してもらうために、量子力学での自由粒子 free particleのエネルギーの式を見てみましょう。自由粒子とは外からなんのエネルギーも与えられていない状態[2]重力やクーロン力が無視でき、束縛されていない状態(=位置エネルギーが0)のことの粒子で、運動エネルギーの式だけで書き表されます。
\begin{aligned}
E=\frac{\hbar^2 \boldsymbol{|k|}^2}{2m} \quad [\text{J}] \quad(=[\text{kg}\cdot \text{m}^2/\text{s}^2)
\end{aligned}導出は省略しますが、別の記事で詳しくまとめる予定ですのでお待ちください(製作中)。
\hbarはディラック定数といい、「エイチバー」と読みます。ディラック定数はプランク定数(h=6.62607015\times10^{-34}[\text{J} \cdot \text{s}] )という定数を2\piで割った値です。kは波数といわれる変数で、単位長さあたりに含まれる波の数を表します(波数の説明)。波数は三次元を伝搬する波動の進行方向を表すベクトルでもあるので上の式では太字にしています。
それでは単一電子のエネルギーを求めてみます。電子が1240nmの波長を持っていたとすると電子のエネルギーは
E=2.298\times10^{-25} \quad\text{J}です。
\begin{aligned}
E& =\frac{\hbar^2 \boldsymbol{|k|}^2}{2m} \\[3mm]
& =\frac{h^2 (\boldsymbol{|k|}/2\pi)^2}{2m} \\[3mm]
& =\frac{h^2}{2m\lambda^2}\\
& = \frac{(6.626\times10^{-34})^2}{2\times9.109\times10^{-31} \times (1240\times10^{-9})^2} \\[3mm]
& \approx1.567\times10^{-25} \quad \text{J} \\[3mm]
\lambda&=\frac{2\pi}{|\boldsymbol{k}|^2}[\text{m}]
\end{aligned}ディラック定数(10^{-34})が式に入っているので、とっても小さい値であることがわかります。
これほどまでに小さいエネルギーの細かな違いに注目するのが量子力学です。
続いて、古典力学を振り返りましょう。古典力学では運動エネルギーはこの式でした。
E=\frac{\boldsymbol{|p|}^2}{2m}(=\frac{1}{2}m \boldsymbol{|v|}^2)\quad[\text{J}] \\ [5mm]運動量や速度は連続量なので、速度に対するエネルギーは滑らかな二次曲線になります。(横軸と縦軸の具体的な値は気にしないでください。)

しかし、量子力学の世界は非常に小さなエネルギーを見ているので、二次関数的な概形になりつつもそのエネルギーは飛び飛びの値になります。
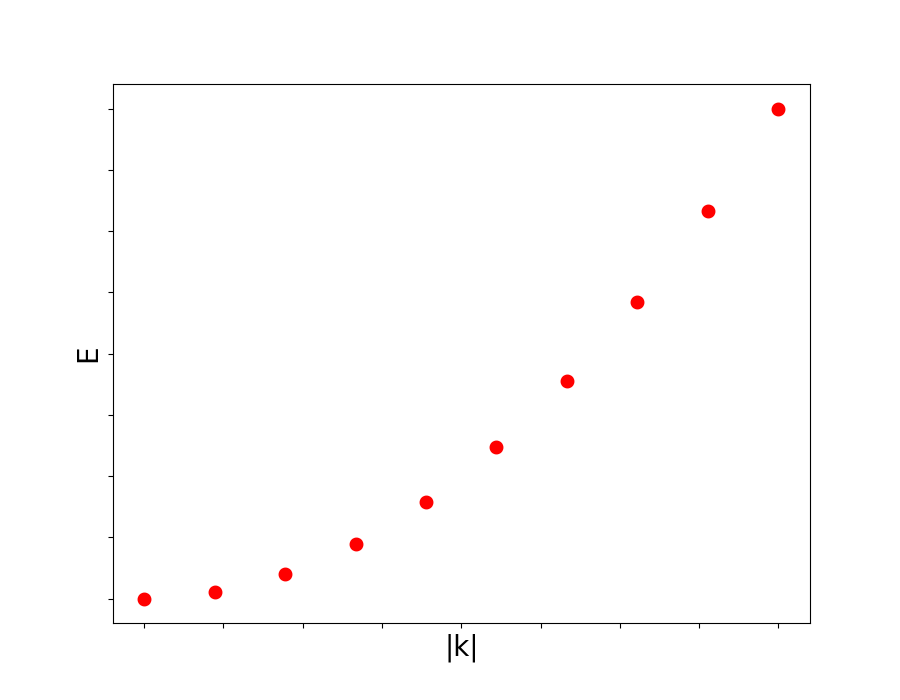
エネルギーが大きい古典物理の世界では離散的にエネルギーが分布していてもあたかも連続的に見えます。我々の視点からはその離散性を確認することは難しいので無視しても問題ありません。しかし、量子力学の世界では離散性を無視できないほど小さな世界を取り扱うので、物質などを離散化された量子で見る必要があります。
波数 Wave number
電子のエネルギーを求めるときに「波数」という言葉が出てきました。波数は電磁気学などの波動を扱う際に登場し、単位長さあたりに含まれる波の数を表す量ですが、初見ではイメージが湧きにくい変数の一つです。
そこで、高校で習う波の式を変形して確認することにします。まず空間中を伝搬する波はこう書けました。
x=A\text{sin} \left( 2\pi(\nu t-\frac{x}{\lambda}) \right) \\ [2mm]\nuは波の周波数です。周波数といえばfがおなじみですが、量子力学や光学の分野では\nuで置く場合が多いです。
この式をちょっと変形します。
\begin{aligned}
x
&=A\text{sin}\left(2\pi(\nu t-\frac{x}{\lambda})\right) \\
&=A\text{sin}(\omega t-kx) \\
&\omega=2\pi\nu[\text{rad/s}], \quad k=\frac{2\pi}{\lambda}[\text{1/m}]
\end{aligned}変形した後の\omegaは角周波数といいます。三角関数や物理の波の運動と関連して学んだ人も多いのではないでしょうか。そしてkが波数です。波数は上の式の通り、波長と逆数の関係にあるので、すでに説明した通り単位長さあたりに含まれる波の数を表します。
波数の定義式を使えば、波長550[nm]の緑色の光の波数は
k
=\frac{2\pi}{550\times10^{-9}} \approx11.4\times10^6 \quad [1/ \text{m}] と求められます。大体1千万[1/ \text{m}]なのでとっても大きい数ですね。しかし、求めた波数を使って量子力学のエネルギーを求めると、\hbar(10^{-34})がつくので最終的に非常に小さい値になります。
なぜ、運動エネルギーに速度ではなく波数を使うのかというと、量子は波動の性質をもつ上に、観測によって存在位置が変化するからです。速度は位置を微分して求めるので連続的な運動では適切な値が得られますが、観測の度に位置が変化する量子では観測した瞬間の速度は0になって運動エネルギーを求められません。
このお話は、位置と運動量は同時には決められないというハイゼンベルグの不確定性関係へと続いていきますが、こちらも詳しくは他の記事にまとめる予定です(製作中)。
量子を観測すると位置が変化するという不思議な現象はこちらの記事にまとめました。
 「ある」と「ない」が一つの不思議な世界/シュレディンガーの猫とは
「ある」と「ない」が一つの不思議な世界/シュレディンガーの猫とは 物理ではギリシャ文字もたくさん登場するのでついでに確認しておきましょう。
 数学で使う海外の文字・書体をLaTeXで入力する方法【ギリシャ文字、オープンフェイス、ヘブライ文字、ドイツ文字】
数学で使う海外の文字・書体をLaTeXで入力する方法【ギリシャ文字、オープンフェイス、ヘブライ文字、ドイツ文字】 量子の種類
量子の代表例として電子と光子を挙げましたが、他に量子はないのでしょうか。
実は、さまざまな波動や振動を量子と見なすことができます。
下にいくつか列挙してみました。
- 電子 electron
- 光子 photon : 光の量子化
- フォノン phonon : 格子振動の量子化
- プラズモン plasmon : プラズマ振動の量子化
- マグノン magnon : 磁気モーメントの振動の量子化
- ポーラロン polaron : 分極の量子化
それぞれの詳しい意味についてはシュレディンガー方程式を解かないと想像しにくいので省略します。今はなんとなくこんなのがあるんだなー程度でOKです。今後、フォノンについては記事を作成する予定ですのでお楽しみに(製作中)。
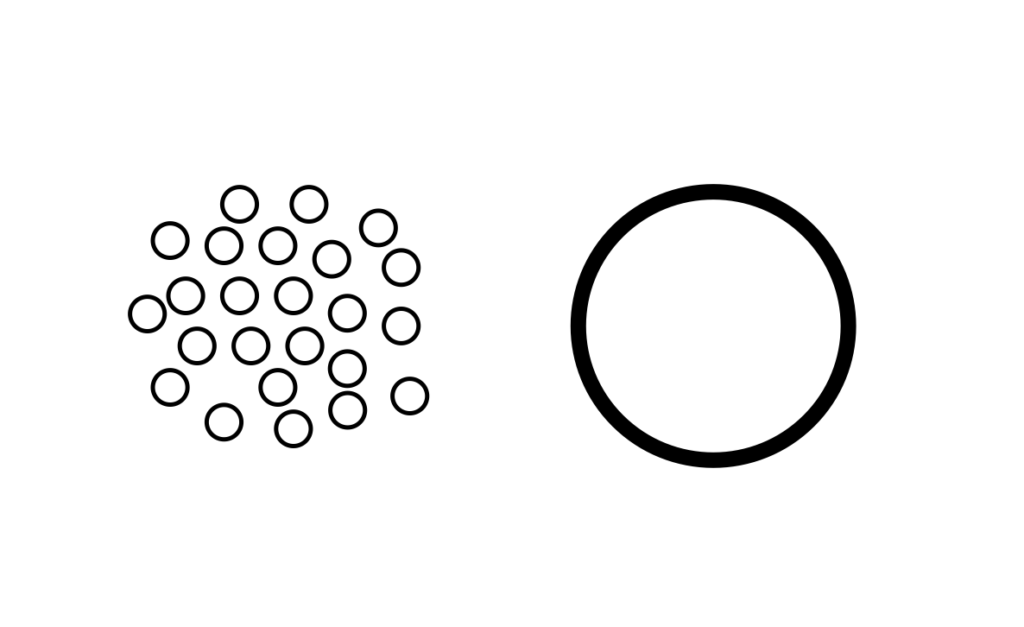
上に挙げた量子たちは、全体的に波動や振動を量子化しているものが多いです。古典物理学では波動だったはずなのに、量子化によって粒のように一つずつ数えることができるようになります。これが量子化の最大の特徴です。
“波動の量子化”を簡単に説明すると、下の画像のような山のような波を一つの粒子であるかのように見ることです。この波はいろんな波が重ね合わさって一つの塊(束)のように存在しているので波束 wave packetと呼ばれます。
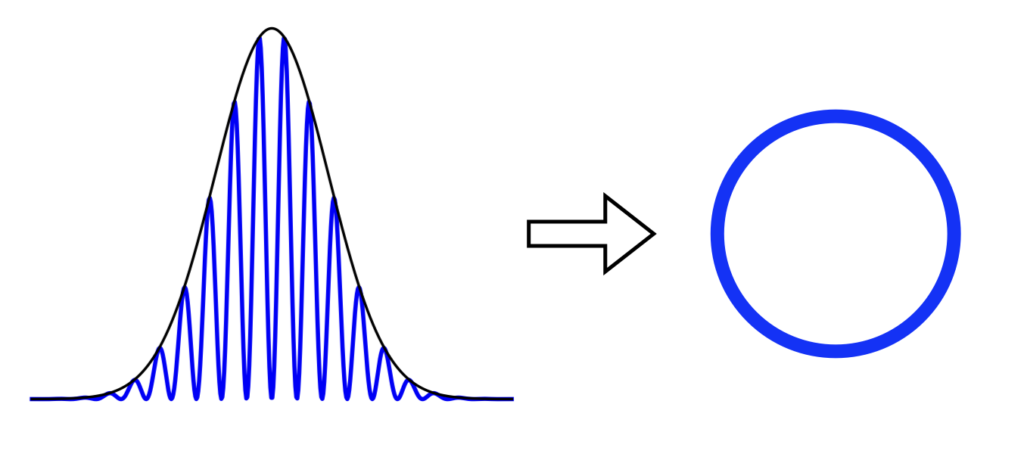
量子化すると古典物理学で使われていた名称とは別の固有名詞で呼ばれるようになります。例えば、光はもともとlight ですが量子化すると光子 photon と呼ばれるようになります。他の量子も同様ですが、電子 electronだけはもともと古典的に粒だと思われてきたので量子化しても呼び方はそのままです。
かといって、量子は必ずしも「空間的に」飛び飛びで粒子のように存在している必要はありません。エネルギーの値が離散的であるならそれを量子とみなすこともできます。
ここまで量子の持つ性質や種類を紹介してきました。なんとなく量子力学が見ている世界の規模感や量子化などの言葉の意味が理解できたのではないでしょうか。続いてちょっと話はそれますが、量子力学が見ている世界のエネルギーについて説明しましょう。
まとめ
今回の量子に関する記事のまとめです。最低限これだけ覚えておきましょう。
- 量子は波と粒の性質を合わせ持った小さな物質やエネルギーである。
- 粒子や波動を量子力学で扱えるように再定義することを量子化という。
- 量子のエネルギーは非常に小さくその値は離散的である。
よければ記事の一番下にある関連記事もぜひご覧くさい。この記事と合わせて読めば量子力学全体の理解度がグッと上がります。
最後に著者の雑記もご覧ください。
雑記:著者にとっての物理学
突然ですが、みなさんは身の周りの物体を限界までズームしたらどうなるんだろうと想像したことはあるでしょうか。私は幼い頃、よくグラスに入ったジュースと空気の境目をボーッと近くで眺めたり、鉛筆で描いた線に目を近づけて、極限まで小さく見ていったらどういうふうに見えるのかなと想像していました(昔から近視でしたので)。
そんな私にとって物理学は身近に溢れる素朴な疑問を答えてくれる学問でした。決して試験で得点をとるためではなく、ごく当たり前の現象への「なぜ」が根源的なモチベーションでした。今でもそれが学びの意義だと思っています。
グラスの水面や鉛筆で引っ張った線は私たちの目には滑らかな直線や曲線に見えますが、細かく見ると原子が周期的に並んでいて凹凸があるでしょう。一方で原子は熱(温度)がありますから、同時に波のように振動しています。さらに細かく見ると、原子は原子核と電子という粒子からできていて、でも電子をじっと見ていると粒ではなく波でもあります。
このように考えていくと小さい世界になるにつれて波と粒子の性質は交互に登場し、その区別や境界はだんだんぼやけていきます。そういった視点に立てば、波と粒子はお互い切り離されるべきではありません。そして電子一つを見るほどズームした時の世界を説明した学問が量子力学なのではないでしょうか。
量子力学よりさらに小さい領域では素粒子物理学 particle physicsやひも理論 string theoryといわれる理論が適用されます。前者は素粒子というだけあって粒子的な見方、ひも理論は波動的な見方に立っているはずです。
粒子・波とは何か、空間・時間とは何かといった哲学的な問いにもいつか物理学が答えを出してくれるかもしれません。今後の学問の発展に期待したいと思います。
本記事は量子の世界をより身近に感じてもらうために厳密さに欠ける内容も入っています。
当サイトで取り上げた記事のほか、Twitter でもさまざまな情報を発信していますのでよろしければフォローをお願いします。
マサ: @masa_fpp03

