波動関数の意味とその性質【状態・重ね合わせの原理】

量子力学のシュレディンガー方程式を解くと波動関数 wave functionという関数が求められます。
波動関数は電子や光がどれくらい広がって存在しているかを表しています。また、重ね合わせの原理 principle of superpositionという基本原理に従って、「ある」と「ない」が共存した不確定な状態を作り出すことができます。

そんな波動関数は、量子力学の最も基礎的な方程式であるシュレディンガー方程式と深い関係があるので、今回はシュレディンガー方程式の簡単な説明から始めます。
「簡単」に説明するためにも、この記事ではシュレディンガー方程式を詳しく解かずに、高校物理までの知識でわかるように解説していきます。

波動関数と状態の説明

シュレディンガー方程式の説明

最も単純なシュレディンガー方程式は次のように書き表されます。

\left( \frac{\boldsymbol p^{2}} {2m}+V(\boldsymbol r) \right)\phi(\boldsymbol r)
=E\phi(\boldsymbol r)

それぞれの文字の意味は以下のリストにまとめています。

• \boldsymbol{p}：量子の運動量
• m：量子の質量
• V(\boldsymbol{r})：ポテンシャルエネルギー
• E：量子のエネルギー
• \phi(\boldsymbol r)：波動関数

この式は、量子現象を説明するために天下り的^[1]数学や物理学で、なぜか分からないが天から降って湧いたように導入するとうまくいく式や解法のことに登場した方程式で、古典力学のニュートンの運動方程式^[2]F=maに相当する基本方程式です。

それでは、シュレディンガー方程式の簡単な説明をします。

運動エネルギー

はじめに、左辺第1項 \boldsymbol{p}^2/2mは、量子力学の世界での粒子の運動エネルギー kinetic energyを表し、例えば電子などが該当します。運動量\boldsymbol{p}は、ベクトルであることを表すために太字で書きました。

運動エネルギーは高校で習った運動量の関係式 \boldsymbol{p}=m\boldsymbol{v}を使って、次のような見慣れた形に変形できます。

\frac{\boldsymbol p^{2}} {2m}=\frac{1}{2}m \boldsymbol{v}^2

ただし量子力学の世界では、電子は波であり粒子であるため上の式が成り立つような「速度」を定義できず、方程式を解く際には使えないので注意が必要です。
具体的にどうするのかについては、別の記事で解説しましょう。(制作中)

位置エネルギー

左辺2項目のV(\boldsymbol {r})は位置エネルギー potnetial energyといいます。位置エネルギーは、量子力学ではポテンシャルエネルギーと呼ぶ場合が多いのですが、こちらの記事では位置エネルギーで統一することにします。位置エネルギーの項には、電場^[3]電界や磁場^[4]磁界によるエネルギーが代入されます。

具体的に位置エネルギーの例を挙げると、原子核に束縛される電子の運動を計算するには、電子と原子核のクーロン力に起因するエネルギーを代入します。逆に、外から何のエネルギーも加えられていない電子の運動を計算する場合は、位置エネルギーに0を代入します。
位置エネルギーがどんな式で表されるかによって、シュレディンガー方程式の形も大きく変化します。

これ以上解説すると本筋から脱線するので、この記事では具体的な形には立ち入りらず先に進みます。

エネルギー固有値

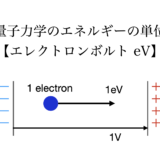
右辺のEはエネルギー固有値 energy eigenvalueと呼ばれ、エネルギーを単位に持ちます。シュレディンガー方程式の左辺が運動エネルギーと位置エネルギーの和^[5]力学的エネルギーで表されるので、右辺もエネルギーを単位に持つ量になります。量子力学の世界ではエネルギーがあまりに小さいので、単位はジュール[\text{J})]ではなくエレクトロンボルト[\text{eV}]という単位を使います。

波動関数

最後に、ギリシャ文字の\phiファイ(\boldsymbol{r})が波動関数を表します。量子力学以前の物理学である古典物理学に従うなら、全エネルギーは両辺の波動関数を消去した

\frac{\boldsymbol p^{2}} {2m}+V(\boldsymbol r)
=E

のような力学的エネルギーで書き表されていました。しかし、量子力学ではわざわざ波動関数を両辺に掛けた方程式を解かなくてはなりません。その理由を次の章で解説します。

量子の世界では観測の度に結果が変わる

波動関数を考慮する理由の一つは、測定するたびに得られる位置や運動量などの結果が変わるからです。

普段の生活や大学での実験など、私たちが長さ、質量、エネルギーなどの物理量 physical quantityと言われる量を観測するときは、外部から変化を促す力やエネルギーが加わっていない、または無視できるほど小さい場合、測定量は常に一定になります。

測定の度に物理量が変わってしまうことを、私たちの身近な物理量の一つである体重を例に説明しましょう。皆さんは体重を計測する際に、体重計に乗って数値を読み取ると思います。その時、体重計の指す値は一定のはずです。日頃ハードなトレーニングに励むアスリートでさえ、一日の体重変化は数kg程度に収まります。ましてや、体重計に乗ったまま数値を見るたびに体重が変動することはなく、したがって、観測するという行為そのものが物理量である体重を変化させることはありません。

しかし、量子力学の原理にのっとると、そのような現象が現実に起きてしまうことになります。
体重の変化は決して誤差の範囲ではなく、さっきは50kgだったのに今度測ったら10kgだった、というほど大幅に値が変わります。

もう少し物理学に沿った説明をするなら、熱力学が良い例の一つです。高校で勉強する理想気体の状態方程式 equation of stateは以下のような式です。

PV=nRT

• P：圧力
• V：気体の占める体積
• n：物質量
• R：気体定数
• T：温度

この式の圧力Pや体積Vといった物理量は、観測・測定自体の影響で変化することはありません。しかし原子一つが見えるほど小さな、量子の世界でも状態方程式があるとすると、観測の度に測定値は変化していくことになります。

波動関数とは状態そのものを表す

観測するたびに物理量が変化してしまう問題を解決するためには、質量、長さ、エネルギーなどの物理量全体を内包する「状態」そのものを表現した関数を方程式に組み込むことで解決できます。そのために導入された関数のことを波動関数と呼びます。
つまり、波動関数とは「物理量の背後にある状態そのもの」といえるような関数です。

いきなり「波動関数=状態」と言われてもよく分からないかも知れないので、記事を読んでいる画面の前のあなたにちょっとしたクイズを出しながら、量子力学の状態(=波動関数)の正体をつかんでいただこうと思います。

突然ですが、今から下の箇条書きの情報を元に、それらの情報と合致する「元素」が何なのか、少しの時間推測してみてください。

• 質量数：186.2
• 原子半径：1.37[\text{\AA}]
• 特筆点：地球上で最も希少
• 生成方法：超新星爆発

実は、みなさんが行った元素を特定するまでのプロセスは、量子力学の状態、物理量、観測と対応関係にあります。

• 元素の情報→物理量
• 情報から元素を調べる行為→観測
• 元素の名称や元素自体→状態(波動関数)

はじめに、「元素の情報」は元素の断片的な性質を表しており、量子力学の「状態」の一側面である「物理量」に相当します。次に様々な断片的な元素の情報から、元素の正体を調べる行為が量子力学の「観測」です。観測によって様々な物理量を調べ、状態を求めるために必要な要素を集めます。最後に、推測した元素の名称や元素そのものが、量子力学の「状態」に相当します。

別の例で言い換えると、量子力学では数式を使ってバラバラに散らばっている「物理量」というピースを「観測」によって一つずつ調べ、「状態」というパズルを解いていきます。そして、求めるパズルに相当するのが「状態」でありシュレディンガー方程式の「波動関数」ということです。

クイズと量子力学の明らかな違いとして注意すべき点が、クイズには明確に正解が存在し、私たちは正解である元素の名前を知ることができます。しかし、量子力学では観測によって得られる結果は物理量であって状態ではなく、状態そのものを観測することはできません。
したがって、波動関数の実体を直接観測することができず、あくまで物理量を元に波動関数や量子力学的な性質を推測することになります。このことは、量子力学が波動関数を当てるクイズだとすると、クイズの正解がはっきりと存在しない、あるいは複数存在することに相当します。

また、物理量すら観測によって容易に変化してしまうのが量子力学の世界です。古典物理学では、物理量は観測によって変化せず常に一定です。一方、量子力学の理論によると、例えばあなたが私の趣味を聞いたとき、最初は「サーフィンが好き」といっていたにもかかわらず、5秒後に同じ質問をすると「スノーボードが好き」と返されるというようなことが、現実に起こり得ます。
こうした量子力学の不可思議な性質は、プラトンの洞窟の比喩 Allegory of the caveや思考実験の中国語の部屋、哲学的ゾンビ Philosophical zombieと共通点があるように思います(クリックするとWikipediaに飛びます)。

量子力学では状態を筆頭に、ある種のブラックボックスになっている概念が多く、それらに多様な解釈が生まれています。本記事でも波動関数に対する代表的な解釈として、ボルンの確率解釈 Born’s stochastic interpretationという、量子力学で広く支持されている解釈を次節で紹介しています。

ボルンの確率解釈とは

前節で説明したように、私たちは量子の状態そのものを観測することができません。
では、実体の捉えられない状態＝波動関数も、物理学者が作り出した単なる机上の空論に過ぎないのでしょうか。
現代の量子力学は、そうした疑問に一つの解釈を提示しています。その解釈の一つが、前節で触れたボルンの確率解釈 Born’s stochastic interpretationです。

ボルンの確率解釈によると、波動関数の絶対値を取って二乗した値が、その地点に粒子が存在する確率密度を表しています。確率密度とは、非常に狭い領域の確率のことです。
波動関数は一般に実数と虚数からなる複素数です。なぜ複素数かというと、波動関数には私たちが観測できる実数の他に、私たちが観測できない虚数の成分も含まれていると考えられたからです。しかし、複素数である波動関数に対して絶対値をとって二乗すると、虚数の成分が消えて私たちにも観測できるようになります。その値が粒子の存在確率だとする解釈が、ボルンの確率解釈です。

ある地点での粒子の存在確率を \rhoロー(x,y,z)、私たちが住む三次元空間x,y,zでの波動関数を\phi(x,y,z)として、ボルンの確率解釈を式に表すと下のように書けます。

\begin{aligned}
\rho(x,y,z)
& =\phi^*(x,y,z)\phi(x,y,z) \\[4mm]
&=|\phi(x,y,z)|^{2}
\end{aligned}

上の式では、波動関数\phi(x,y,z)とその複素共役\phi^*(x,y,z)を掛け合わせた式を計算しており、それがある地点の粒子の存在確率と等しいことを表しています。

波動関数とは何かを説明したところで、次章では波動関数の持つ特異な性質を紹介しましょう。

波動関数の性質

規格化：波動関数の値域を揃える

ボルンの確率解釈を説明した際に、波動関数の絶対値の二乗はその地点の確率密度\rho、つまり1つの粒子が狭い領域で存在する確率を表すと説明しました。
\rhoはあくまで確率密度なので、粒子がより大きな3次元空間に存在する確率P(x,y,z)を求めるには、x軸、y軸、z軸方向に積分する必要があります。すなわち、\rhoに対して下に書いたような積分を行います。

\begin{aligned}
P(x,y,z)
& =\int_{z_1}^{z_2}\int_{y_1}^{y_2}\int_{x_1}^{x_2}\rho(x,y,z)dxdydz\\
& =\int_{z_1}^{z_2}\int_{y_1}^{y_2}\int_{x_1}^{x_2}\phi^*(x,y,z)\phi(x,y,z)dxdydz
\end{aligned}

P(x,y,z)は確率を表すので値域は0~1で、全区間で積分すると1になるはずですが、波動関数自体の値域には制限がなく、0~1であることの方が少ないです。波動関数は私たちに観測できない量として導入された関数なので、それを反映するかのように値域の制約はありません。

そこで、\rho(x,y,z)を3次元空間全体で積分した値Nで割り、確率Pの値域を0~1にそろえてあげます。そのことを規格化 normalizationまたは正規化と言います(どちらも同じ意味です)。

Nは規格化定数 normalization constantといい、Nを求めるためには下に書いた計算をします。積分時にdxdydzと毎回書くのは冗長なので、まとめてd\boldsymbol{r}と書くことにします。

\begin{aligned}
&N\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\rho(x,y,z)dxdydz=1 \\[4mm]
& N\int_{-\infty}^{\infty}\rho(\boldsymbol{r})d \boldsymbol{r}=1\\[4mm]
&N\int_{-\infty}^{\infty}\phi^*(\boldsymbol{r})\phi(\boldsymbol{r})d\boldsymbol{r}=1 \\[4mm]
\therefore \quad
&N=\frac{1}{\int_{-\infty}^{\infty}\phi^*(\boldsymbol{r})\phi(\boldsymbol{r})d\boldsymbol{r}}
\end{aligned}

積分範囲の\inftyは全区間という意味です。
(広義積分を覚えている方は、上の式のように極限を使わない書き方に違和感を覚えるかもしれません。しかし、物理学の世界では毎回\text{limit}を書くのは面倒なので基本的にこのように書きます)

細かい計算をしたいときには、各軸ごとに積分範囲を決めて積分を実行します。

積分すると自動的に規格化されるように、あらかじめ波動関数を下のように書くこともあります。

\frac{1}{\sqrt{N}}\phi(\boldsymbol{r})

上の波動関数を規格化した波動関数といいます。
\phi(\boldsymbol{r})が規格化されているかどうかで、細かな計算結果に影響することがあるため、規格化定数の有無には注意する必要があります。とはいえ、「\phiは規格化されている」などとことわって\sqrt{N}は書かないことも多くあります。

演算子：物理量の確率を求める

前節までは波動関数で粒子の存在確率がどのように表現されるかを説明しました。似たような数式で、粒子の存在確率だけでなくエネルギーなどの物理量(観測量)の確率も表現することができます。その場合、単純に波動関数とその複素共役を掛けて積分するのではなく、物理量に対応する特別な記号を、波動関数で挟んで積分します。

例えば、ある物理量Aの期待値\langle A(\boldsymbol{r})\rangleを求めるためには、このような計算をします。

\begin{aligned}
\langle A(\boldsymbol{r})\rangle
& =\int_{-\infty}^{\infty}\phi^*(\boldsymbol{r})\hat{A}\phi(\boldsymbol{r})d\boldsymbol{r}
\end{aligned}

\hat{A}は演算子 operatorといわれる記号で、単なるAとは異なります。文字の上にある記号は「ハット」といい、\hat{A}は「エーハット」と読みます。演算子というと四則演算子^[6]+, -, \times, \divを思い浮かべますが、量子力学の演算子はどちらかというと微分演算子を想像するのが分かりやすいと思います。

例として下の式を使って説明します。

\frac{d}{dx}e^{ax}=ae^{ax}

上の式はe^{ax}を微分した結果、元のe^{ax}の係数にaが掛かっています。
見方を変えると、e^{ax}という関数に演算子を掛ける(作用させる)ことで、aという値が出力値として得られたように見えます。量子力学の演算子も同じように、演算子の後ろにある関数に何らかの操作を加えます。先ほどの式では\hat{A}は\phi(\boldsymbol{r})に何らかの操作を行う演算子です。

量子力学では同じような文字でも意味が微妙に違う場合があります。今回の例では

• A：物理量
• \langle A(\boldsymbol{r})\rangle：物理量の期待値
• \hat{A}：物理量を求めるための演算子

がそれぞれ意味合いが異なりますので注意しましょう。

内積：波動関数の類似性を調べる

波動関数が規格化されている(規格化定数Nが波動関数に含まれている)とすると、全空間の波動関数の確率はこのように書けます。

\begin{aligned}
\int_{-\infty}^{\infty}\phi^*(\boldsymbol{r})\phi(\boldsymbol{r})d\boldsymbol{r}=1
\end{aligned}

上の式のように、何らかの関数を掛け合わせてから全空間で積分した値を内積 inner/dot productといいます。規格化定数を求めるために行なった計算は、実は波動関数の内積を計算する式でもあります。

内積という言葉から連想されるように、関数の内積はベクトルの内積と根本的には同じ計算をしており、二つの関数やベクトルがどれくらい似通っているかを表しています。

\begin{aligned}
\boldsymbol{A} \cdot \boldsymbol{B}
&=
\begin{pmatrix}
-1 \\
-2 \\
3 \\
\end{pmatrix}
\cdot
\begin{pmatrix}
4\\
5\\
6\\
\end{pmatrix}
\\
&=(-1)\times4+(-2)\times5+3\times6 \\
&=4
\end{aligned}

関数もベクトルの内積と同じ計算であることを想像してもらうために、\phi(\boldsymbol{r})が無限の成分をもつベクトルだと思って、内積を計算してみます。
すると、ベクトルの内積は下のような成分同士を掛けた総和になります。

\begin{aligned}
\phi^* \cdot \phi
&=
\begin{pmatrix}
...\\
\phi^*_1\\
\phi^*_2\\
\phi^*_3\\
...\\
\end{pmatrix}
\cdot
\begin{pmatrix}
...\\
\phi_1\\
\phi_2\\
\phi_3\\
...\\
\end{pmatrix}
\\
&=\sum_{n=-\infty}^\infty \phi^*_n\phi_n
\end{aligned}

このように書き下すと、本来違う定義であったはずの関数の内積とベクトルの内積が同じような式に見えませんか？
もしもベクトルのnの刻み幅が微少量なら、積分で書いた内積の式と一致します。よって、ベクトルの内積も関数の内積も本質的には同じ計算をしています。波動関数が規格化されていると、内積の計算で値が0~1になるので、どれほど波動関数が似通っているのかわかりやすいです。この場合は内積が1なので波動関数同士が同じであることを示しています。

内積の定義は本来、関数の一方に複素共役を掛ける必要はないのですが、量子力学では波動関数が複素数なので虚部を消すために(ボルンの確率解釈を満たすために)、複素共役を取った関数と元の関数を掛けて計算します。

内積は異なる波動関数\phi_1^*(\boldsymbol{r})、\phi_2(\boldsymbol{r})に対しても同じように計算することができます。そしてもし、

\begin{aligned}
\int_{-\infty}^{\infty}\phi_1^*(\boldsymbol{r})\phi_2(\boldsymbol{r})d\boldsymbol{r}
=0
\end{aligned}

のように何らかの関数の内積が0になる場合、「関数が直交する」といいます。関数も直交している場合、関数同士が同じ成分を持たないことを示しています。

さて、波動関数の話に戻りますが、異なる波動関数は一般的には直交していません。しかし、ユニタリー変換 unitary transformationという数学的操作を通して互いに直交した波動関数に変換することができます。
この記事ではこれ以上踏み込みませんが、こちらも他の記事で解説できたらと考えています。(制作中)

重ね合わせの原理：波動関数は足し合わせることができる

波動関数は互いに足し合わせることができ、その性質を重ね合わせの原理 principle of superpositionと言います。重ね合わせの原理を用いると、ある波動関数を別の波動関数の足し合わせで表現できます。
式を使って表現すると、ある波動関数\Phiファイ(\boldsymbol{r})は別の波動関数\phi_1^*(\boldsymbol{r})、\phi_2(\boldsymbol{r})を使って、

\begin{aligned}
\Phi(\boldsymbol{r})=C_1\phi_1(\boldsymbol{r})+C_2\phi_2(\boldsymbol{r})
\end{aligned}

と書けます。C_1、C_2は波動関数の混ざり具合を表す定数です。

波動関数は、直交した波動関数のようにお互いに同じ成分を含まない、全く異なる性質を持った波動関数(状態)同士も重ね合わせることができます。具体的には「上向きスピン」と「下向きスピン」と呼ばれる状態や、異なる電子軌道関数(s軌道、p軌道)などが挙げられます。

また、波動関数は二つだけでなく、理論上は状況に応じて無限個の波を重ね合わせることが出来ます。式で書くと、

\Phi(\boldsymbol{r})=\sum_{n=0}^{\infty}C_n\phi_n(\boldsymbol{r})

のように、無限個の波動関数の重ね合わせで別の波動関数を表現することが出来ます。
このように、ある波動関数を別の二つ以上の波動関数の重ね合わせで書くことを、「波動関数を展開する」といいます。複雑な波動関数を近似する手法として、別の波動関数で展開することが多くあります。波動関数の展開につきましては、代数的なシュレディンガー方程式の解説の際にでまとめようと思います。(制作中)

まとめ

今回は、波動関数の正体とその性質を紹介しました。波動関数の正体とその性質をまとめると次の通りです。

• 波動関数とは状態を方程式に落とし込むために導入された関数
• 直接的に観測できず、代わりに物理量を観測することで推測する
• 二乗して絶対値を取った値が、粒子の確率密度を表す
• 内積によって波動関数同士の類似性がわかる
• 演算子と組み合わせて、物理量の確率を算出する
• 波動関数同士を足し合わせて、別の波動関数を表現できる

このような波動関数の性質を駆使して、量子力学ではさまざまな物理現象を明らかにしていきます。

• どのように波動関数を求めるのか
• 波動関数の性質が量子力学の何に役立つのか
• 物理学として波動関数にはどんな役割があるのか

などにつきましては、計算を行って初めて腑に落ちる部分もあるかと思います。
他の記事にシュレーディンガー方程式の解法をまとめる予定ですので楽しみにお待ちください(製作中)。

本記事は量子の世界をより身近に感じてもらうために厳密さに欠ける内容も入っています。

当サイトで取り上げた記事のほか、Twitter でもさまざまな情報を発信していますのでよろしければフォローをお願いします。

マサ: @masa_fpp03